※早く知りたい方は、「4. まとめ」まで飛ぶことをおすすめします!
三角比の求め方とは?
ここでは、三角形の図を使って示してみましょう!
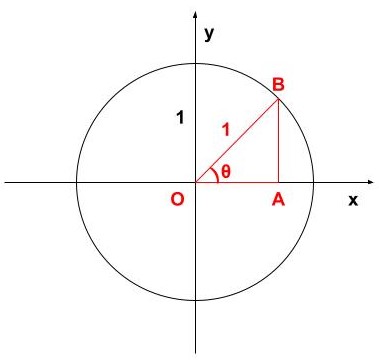
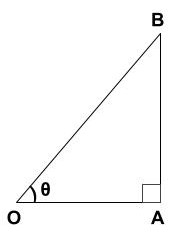
上図のように、半径1の円の中に直角三角形OABを作ります!
直角三角形OABの、直角以外の一つの角をθと置きます!
すると、三角比の公式は以下のようになります!
\begin{eqnarray} \sin θ=AB/OB \end{eqnarray}
\begin{eqnarray} \cos θ=OA/OB \end{eqnarray}
\begin{eqnarray} \tan θ=AB/OA \end{eqnarray}
三角形の角辺を表すと、
- AB→高さ
- OB→斜辺
- OA→底辺
これらを踏まえると、3つの公式は以下のように表せる!
\begin{eqnarray} \sin θ= {\color{red}{高さ}}/{\color{red}{斜辺}} \end{eqnarray}
斜辺を1とすると、\begin{eqnarray} \sin θ={\color{red}{y座標}} \end{eqnarray}
\begin{eqnarray} \cos θ= {\color{red}{底辺}}/{\color{red}{斜辺}} \end{eqnarray}
斜辺を1とすると、\begin{eqnarray} \cos θ={\color{red}{x座標}} \end{eqnarray}
\begin{eqnarray} \tan θ= {\color{red}{高さ}}/{\color{red}{底辺}} \end{eqnarray}
\begin{eqnarray} \tan θ=直線OBの{\color{red}{傾き}} \end{eqnarray}
主要な角度における三角比の値とは?
公式が分かったところで、いくつか具体的な角度を入れて求めてみましょう!
\(\displaystyle θ=30^\circ\)の時、\(\displaystyle \sin θ, \cos θ, \tan θ\)の値を求めよ
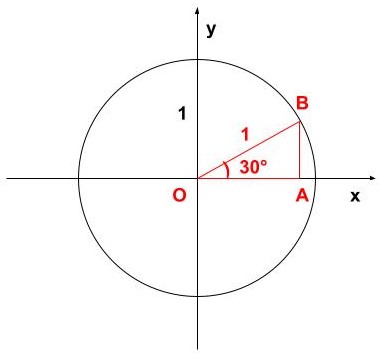
まず、\(\displaystyle OB=1\)から、\(\displaystyle OA\)と\(\displaystyle AB\)の値を求めます!
\(\displaystyle AB:OB:OA={\color{red}{1:2:\sqrt{3}}}\)
よって、
\(\displaystyle AB:1(OBの実際の長さ)=1:2\)より、\(\displaystyle AB=\frac{1}{2}\)・・・①
\(\displaystyle 1(OBの実際の長さ):OA=2:\sqrt{3}\)より、\(\displaystyle OA=\frac{\sqrt{3}}{2}\)・・・②
①、②より、各々の三角比を求めると、以下のようになります!
\begin{eqnarray} \sin 30^\circ=AB/OB=\frac{1}{2}\div1={\color{red}{\frac{1}{2}}} \end{eqnarray}
\begin{eqnarray} \cos 30^\circ=OA/OB=\frac{\sqrt{3}}{2}\div1={\color{red}{\frac{\sqrt{3}}{2}}} \end{eqnarray}
\begin{eqnarray} \tan 30^\circ=AB/OA=\frac{1}{2}\div\frac{\sqrt{3}}{2}={\color{red}{\frac{1}{\sqrt{3}}}} \end{eqnarray}
もう1問やってみましょう!
\(\displaystyle θ=45^\circ\)の時、\(\displaystyle \sin θ, \cos θ, \tan θ\)の値を求めよ
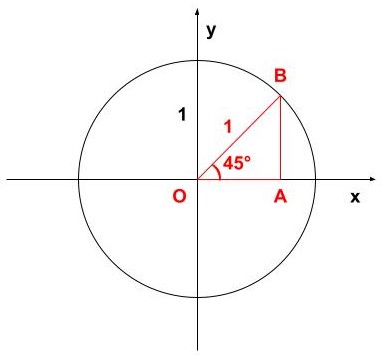
同じく、\(\displaystyle OB=1\)から、\(\displaystyle OA\)と\(\displaystyle AB\)の値を求めます!
\(\displaystyle AB:OB:OA={\color{red}{1:\sqrt{2}:1}}\)
よって、
\(\displaystyle AB:1(OBの実際の長さ)=1:\sqrt{2}\)より、\(\displaystyle AB=\frac{1}{\sqrt{2}}\)・・・①
\(\displaystyle 1(OBの実際の長さ):OA=\sqrt{2}:1\)より、\(\displaystyle OA=\frac{1}{\sqrt{2}}\)・・・②
①、②より、各々の三角比を求めると、以下のようになります!
\begin{eqnarray} \sin 45^\circ=AB/OB=\frac{1}{\sqrt{2}}\div1={\color{red}{\frac{1}{\sqrt{2}}}} \end{eqnarray}
\begin{eqnarray} \cos 45^\circ=OA/OB=\frac{1}{\sqrt{2}}\div1={\color{red}{\frac{1}{\sqrt{2}}}} \end{eqnarray}
\begin{eqnarray} \tan 45^\circ=AB/OA=\frac{1}{\sqrt{2}}\div\frac{1}{\sqrt{2}}={\color{red}{1}} \end{eqnarray}
主要な角度による三角比の値を一気に一覧にすると、以下です!
| 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | |
| sinθ | \(\displaystyle0\) | \(\displaystyle\frac{1}{2}\) | \(\displaystyle\frac{1}{\sqrt{2}}\) | \(\displaystyle\frac{\sqrt{3}}{2}\) | \(\displaystyle1\) | \(\displaystyle\frac{\sqrt{3}}{2}\) | \(\displaystyle\frac{1}{\sqrt{2}}\) | \(\displaystyle\frac{1}{2}\) | \(\displaystyle0\) |
| cosθ | \(\displaystyle1\) | \(\displaystyle\frac{\sqrt{3}}{2}\) | \(\displaystyle\frac{1}{\sqrt{2}}\) | \(\displaystyle\frac{1}{2}\) | \(\displaystyle0\) | \(\displaystyle-\frac{1}{2}\) | \(\displaystyle-\frac{1}{\sqrt{2}}\) | \(\displaystyle-\frac{\sqrt{3}}{2}\) | \(\displaystyle-1\) |
| tanθ | \(\displaystyle0\) | \(\displaystyle\frac{1}{\sqrt{3}}\) | \(\displaystyle1\) | \(\displaystyle\sqrt{3}\) | なし | \(\displaystyle-\sqrt{3}\) | \(\displaystyle-1\) | \(\displaystyle-\frac{1}{\sqrt{3}}\) | \(\displaystyle0\) |
角度が増減!?三角比の「変換公式」の覚え方とは?
具体的な公式としては、以下です!
\begin{eqnarray} \sin (90^\circ-θ)=\cos θ \end{eqnarray}
\begin{eqnarray} \cos (90^\circ-θ)=\sin θ \end{eqnarray}
\begin{eqnarray} \tan (90^\circ-θ)=\frac{1}{\tan θ} \end{eqnarray}
\begin{eqnarray} \sin (90^\circ+θ)=\cos θ \end{eqnarray}
\begin{eqnarray} \cos (90^\circ+θ)=-\sin θ \end{eqnarray}
\begin{eqnarray} \tan (90^\circ+θ)=-\frac{1}{\tan θ} \end{eqnarray}
\begin{eqnarray} \sin (180^\circ-θ)=\sin θ \end{eqnarray}
\begin{eqnarray} \cos (180^\circ-θ)=-\cos θ \end{eqnarray}
\begin{eqnarray} \tan (180^\circ-θ)=-\tan θ \end{eqnarray}
\begin{eqnarray} \sin (180^\circ+θ)=-\sin θ \end{eqnarray}
\begin{eqnarray} \cos (180^\circ+θ)=-\cos θ \end{eqnarray}
\begin{eqnarray} \tan (180^\circ+θ)=\tan θ \end{eqnarray}
\begin{eqnarray} \sin (-θ)=-\sin θ \end{eqnarray}
\begin{eqnarray} \cos (-θ)=\cos θ \end{eqnarray}
\begin{eqnarray} \tan (-θ)=-\tan θ \end{eqnarray}
公式の証明
ここでは、加法定理を使います!
例えば、以下のようになります!
\begin{eqnarray} {\color{red}{\sin (90^\circ-θ)}} &=& \sin 90^\circ\cos θ-\cos 90^\circ\sin θ \\ &=& 1・ \cos θ-0・\sin θ \\ &=& {\color{red}{\cos θ}}\end{eqnarray}
公式
暗記をする際は、
\(\displaystyle 90^\circ, 180^\circ, 360^\circ\)のそれぞれの公式に注目すると、以下のことが分かります!
- \(\displaystyle 180^\circ, 360^\circ\)は、変換後の関数の形が同じ 例:\(\displaystyle {\color{red}{\sin}} (180^\circ-θ)={\color{red}{\sin}} θ \)
- \(\displaystyle 90^\circ\)は、\(\displaystyle \sin⇔\cos\)、\(\displaystyle \tan⇒\frac{1}{\tan}\)と変換される
三角比の「形」のパターンを覚える!
また、変換後の「符号」にも注目です!
符号に注目する際、以下の2つを意識してみてください!
- \(\displaystyle θ\)に具体的な数値を代入
- 三角形の図を書く
例えば、\(\displaystyle θ=60^\circ\)を例に考えてみましょう!
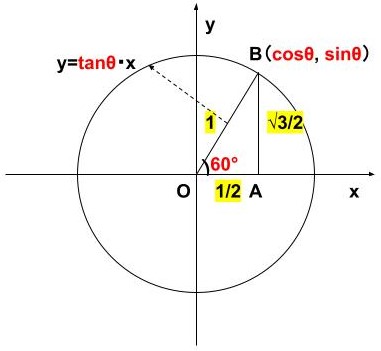
- \(\displaystyle \cos θ\)→\(\displaystyle B\)の\(\displaystyle x\)座標→\(\displaystyle \frac{1}{2}\)
- \(\displaystyle \sin θ\)→\(\displaystyle B\)の\(\displaystyle y\)座標→\(\displaystyle \frac{\sqrt{3}}{2}\)
- \(\displaystyle \tan θ\)→\(\displaystyle OB\)の傾き→\(\displaystyle \frac{\sqrt{3}}{2}\div\frac{1}{2}=\sqrt{3}\)
\(\displaystyle 0^\circ<θ<90^\circ\)、すなわち、\(\displaystyle x\)と\(\displaystyle y\)座標が正のとき、
\(\displaystyle \cos θ{\color{red}{>0}}, \sin θ{\color{red}{>0}}, \tanθ{\color{red}{>0}}\)
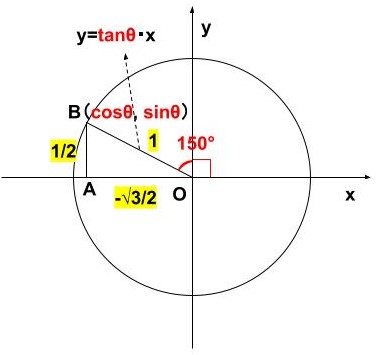
- \(\displaystyle \cos θ\)→\(\displaystyle B\)の\(\displaystyle x\)座標→\(\displaystyle -\frac{\sqrt{3}}{2}\)
- \(\displaystyle \sin θ\)→\(\displaystyle B\)の\(\displaystyle y\)座標→\(\displaystyle \frac{1}{2}\)
- \(\displaystyle \tan θ\)→\(\displaystyle OB\)の傾き→\(\displaystyle \frac{1}{2}\div-\frac{\sqrt{3}}{2}=-\frac{1}{\sqrt{3}}\)
\(\displaystyle 90^\circ<θ<180^\circ\)、すなわち、\(\displaystyle x\)座標が負、\(\displaystyle y\)座標が正のとき、
\(\displaystyle \cos θ{\color{blue}{<0}}, \sin θ{\color{red}{>0}}, \tanθ{\color{blue}{<0}}\)
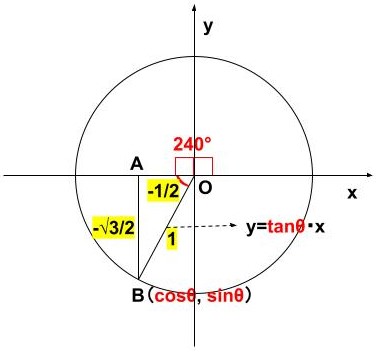
- \(\displaystyle \cos θ\)→\(\displaystyle B\)の\(\displaystyle x\)座標→\(\displaystyle -\frac{1}{2}\)
- \(\displaystyle \sin θ\)→\(\displaystyle B\)の\(\displaystyle y\)座標→\(\displaystyle -\frac{\sqrt{3}}{2}\)
- \(\displaystyle \tan θ\)→\(\displaystyle OB\)の傾き→\(\displaystyle -\frac{\sqrt{3}}{2}\div-\frac{1}{2}=\sqrt{3}\)
\(\displaystyle 180^\circ<θ<270^\circ\)、すなわち、\(\displaystyle x\)座標が負、\(\displaystyle y\)座標が負のとき、
\(\displaystyle \cos θ{\color{blue}{<0}}, \sin θ{\color{blue}{<0}}, \tanθ{\color{red}{>0}}\)
\(\displaystyle θ\)の角度と三角比の「形」、「符号」の関係を表にすると、次のようになります!
| θ(鋭角) |
\(\displaystyle(90^\circ+θ)\) |
\(\displaystyle(180^\circ+θ)\) \(\displaystyle(180^\circ-θ)\) |
\(\displaystyle(270^\circ+θ)\) \(\displaystyle(270^\circ-θ)\) |
\(\displaystyle -θ\) |
| \(\displaystyle \cos θ\) |
\(\displaystyle \sin\) |
\(\displaystyle \cos\) |
\(\displaystyle \sin\) |
\(\displaystyle \cos\) |
| \(\displaystyle \sin θ\) | \(\displaystyle \cos\) | \(\displaystyle \sin\) | \(\displaystyle \cos\) | \(\displaystyle \sin\) |
| \(\displaystyle \tan θ\) | \(\displaystyle \frac{1}{\tan}\) | \(\displaystyle \tan\) | \(\displaystyle \frac{1}{\tan}\) | \(\displaystyle \tan\) |
| 角度 | \(\displaystyle 0^\circ-90^\circ\) | \(\displaystyle 90^\circ-180^\circ\) | \(\displaystyle 180^\circ-270^\circ\) | \(\displaystyle 270^\circ-360^\circ\) |
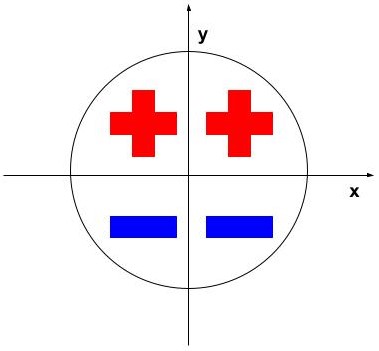
| 座標 | \(\displaystyle x{\color{red}{>0}}\) \(\displaystyle y{\color{red}{>0}}\) |
\(\displaystyle x{\color{blue}{<0}}\) \(\displaystyle y{\color{red}{>0}}\) |
\(\displaystyle x{\color{blue}{<0}}\) \(\displaystyle y{\color{blue}{<0}}\) |
\(\displaystyle x{\color{red}{>0}}\) \(\displaystyle y{\color{blue}{<0}}\) |
| \(\displaystyle \cos θ\) |
正 |
負 | 負 | 正 |
| \(\displaystyle \sin θ\) | 正 | 正 | 負 | 負 |
| \(\displaystyle \tan θ\) | 正 | 負 | 正 | 負 |
まとめ
\begin{eqnarray} \sin θ=AB/OB \end{eqnarray}
\begin{eqnarray} \cos θ=OA/OB \end{eqnarray}
\begin{eqnarray} \tan θ=AB/OA \end{eqnarray}
| 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | |
| sinθ | \(\displaystyle0\) | \(\displaystyle\frac{1}{2}\) | \(\displaystyle\frac{1}{\sqrt{2}}\) | \(\displaystyle\frac{\sqrt{3}}{2}\) | \(\displaystyle1\) | \(\displaystyle\frac{\sqrt{3}}{2}\) | \(\displaystyle\frac{1}{\sqrt{2}}\) | \(\displaystyle\frac{1}{2}\) | \(\displaystyle0\) |
| cosθ | \(\displaystyle1\) | \(\displaystyle\frac{\sqrt{3}}{2}\) | \(\displaystyle\frac{1}{\sqrt{2}}\) | \(\displaystyle\frac{1}{2}\) | \(\displaystyle0\) | \(\displaystyle-\frac{1}{2}\) | \(\displaystyle-\frac{1}{\sqrt{2}}\) | \(\displaystyle-\frac{\sqrt{3}}{2}\) | \(\displaystyle-1\) |
| tanθ | \(\displaystyle0\) | \(\displaystyle\frac{1}{\sqrt{3}}\) | \(\displaystyle1\) | \(\displaystyle\sqrt{3}\) | なし | \(\displaystyle-\sqrt{3}\) | \(\displaystyle-1\) | \(\displaystyle-\frac{1}{\sqrt{3}}\) | \(\displaystyle0\) |
- 証明する方へ
〈加法定理による証明〉
\begin{eqnarray} {\color{red}{\sin (90^\circ-θ)}} &=& \sin 90^\circ\cos θ-\cos 90^\circ\sin θ \\ &=& 1・ \cos θ-0・\sin θ \\ &=& {\color{red}{\cos θ}}\end{eqnarray}
- 暗記する方へ
〈関数の形の暗記〉
| θ(鋭角) |
\(\displaystyle(90^\circ+θ)\) |
\(\displaystyle(180^\circ+θ)\) \(\displaystyle(180^\circ-θ)\) |
\(\displaystyle(270^\circ+θ)\) \(\displaystyle(270^\circ-θ)\) |
\(\displaystyle -θ\) |
| \(\displaystyle \cos θ\) |
\(\displaystyle \sin\) |
\(\displaystyle \cos\) |
\(\displaystyle \sin\) |
\(\displaystyle \cos\) |
| \(\displaystyle \sin θ\) | \(\displaystyle \cos\) | \(\displaystyle \sin\) | \(\displaystyle \cos\) | \(\displaystyle \sin\) |
| \(\displaystyle \tan θ\) | \(\displaystyle \frac{1}{\tan}\) | \(\displaystyle \tan\) | \(\displaystyle \frac{1}{\tan}\) | \(\displaystyle \tan\) |
〈符号の暗記〉
\(\displaystyle \sin θ⇒{\color{red}{y座標}}\)
\(\displaystyle \cos θ⇒{\color{red}{x座標}}\)
\(\displaystyle \tan θ⇒{\color{red}{傾き}}\)




