加法定理とは?
加法定理とは、2つの角度の和あるいは差を使った三角関数を、個々の角度を使った三角関数で表したものです!
ここでの2つの角度を、αとβとします!
早速、公式を6つ紹介します!
\begin{eqnarray} {\color{red}{\sin(α+β)=\sinα\cosβ+\cosα\sinβ}}\end{eqnarray}
\begin{eqnarray} {\color{red}{\sin(α-β)=\sinα\cosβ-\cosα\sinβ}}\end{eqnarray}
\begin{eqnarray} {\color{red}{\cos(α+β)=\cosα\cosβ-\sinα\sinβ}}\end{eqnarray}
\begin{eqnarray} {\color{red}{\cos(α-β)=\cosα\cosβ+\sinα\sinβ}}\end{eqnarray}
\begin{eqnarray} {\color{red}{\tan(α+β)=\frac{\tanα+\tanβ}{1-\tanα\tanβ}}}\end{eqnarray}
\begin{eqnarray} {\color{red}{\tan(α-β)=\frac{\tanα-\tanβ}{1+\tanα\tanβ}}}\end{eqnarray}
覚え方・語呂合わせ
それでは、以上の6つの公式をどのように覚えるのか?
ここでは、語呂合わせがあるので簡単に暗記できます!
以下は、全てα+βの時の語呂合わせです!
α-βは、α+βの符号を入れ替えるだけでOKです!
sinの語呂合わせ
\begin{eqnarray} \sin(α+β)={\color{blue}{\sinα}}{\color{yellow}{\cosβ}}+{\color{yellow}{\cosα}}{\color{blue}{\sinβ}} \end{eqnarray}
咲いたコスモス コスモス咲いた
cosの語呂合わせ
\begin{eqnarray} \cos(α+β)={\color{yellow}{\cosα}}{\color{yellow}{\cosβ}}{\color{red}{-}}{\color{blue}{\sinα}}{\color{blue}{\sinβ}} \end{eqnarray}
コスモスコスモス 咲かない咲かない
tanの語呂合わせ
\begin{eqnarray} {\color{red}{\tan(α+β)=\frac{{\color{red}{\tanα}}+{\color{red}{\tanβ}}}{{\color{blue}{1}}{\color{yellow}{-}}{\color{red}{\tanα}}{\color{red}{\tanβ}}}}}\end{eqnarray}
いーたたたた!
東大で出題!?加法定理の証明方法
1999年に、東大において加法定理の証明問題が出題されたことがあります!
(文理共通で、「一般角に対してsin(α+β)とcos(α+β)を証明せよ!」という問題です。)
それくらい、加法定理の証明はとても重要です!
ただ、証明方法もすごく簡単です!
なぜなら、cos(α-β)が証明できれば、芋づる式に他の5つも証明できるからです!
早速、cos(α-β)から証明してみましょう!
cos(α-β)の証明
まず、座標平面上に半径1の円と点A (cosα , sinα)、点B (cosβ , sinβ)を描きます!
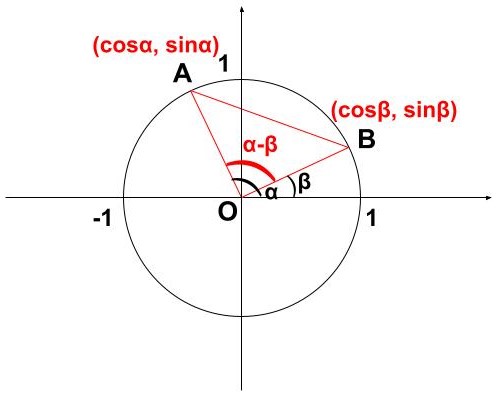
上の、辺ABを次のように2通り求めます!
2点間の距離の公式より、
\begin{eqnarray} AB^{2} &=& (\cosα-\cosβ)^{2}+(\sinα-\sinβ)^{2} \\ &=& \cos^{2}α-2\cosα\cosβ+\cos^{2}β+\sin^{2}α-2\sinα\sinβ+\sin^{2}β \\ &=& 2-2(\cosα\cosβ+\sinα\sinβ)・・・① \end{eqnarray}
余弦定理より、
\begin{eqnarray} AB^{2} &=& OA^{2}+OB^{2}-2・OA・OB・\cos(α-β) \\ &=& 1^{2}+1^{2}-2・1・1・\cos(α-β) \\ &=& 2-2\cos(α-β)・・・② \end{eqnarray}
①、②より、
\begin{eqnarray} 2-2(\cosα\cosβ+\sinα\sinβ) &=& 2-2\cos(α-β) \end{eqnarray}
よって、
\begin{eqnarray} {\color{red}{\cos(α-β)=\cosα\cosβ+\sinα\sinβ}}\end{eqnarray}
残り5つの公式の証明
cos(α+β)の証明
cos(α-β)の、\(\displaystyle {\color{red}{β}}\)を\(\displaystyle {\color{red}{-β}}\)に入れ替える!
\begin{eqnarray} \cos(α+β) &=& \cosα\cos(-β)+\sinα\sin(-β) \end{eqnarray}
\begin{eqnarray} \cos(-β)=\cosβ \sin(-β)=-\sinβ\end{eqnarray}
よって、
\begin{eqnarray} {\color{red}{\cos(α+β)=\cosα\cosβ-\sinα\sinβ}}\end{eqnarray}
sin(α-β)の証明
\(\displaystyle \cos(α+β)\)の、\(\displaystyle {\color{red}{α}}\)を\(\displaystyle {\color{red}{\frac{π}{2}-α}}\)に入れ替える!
\begin{eqnarray} \cos(\frac{π}{2}-α+β) &=& \cos(\frac{π}{2}-α)\cosβ-\sin(\frac{π}{2}-α)\sinβ \end{eqnarray}
\begin{eqnarray} \cos(\frac{π}{2}-α)=\sinα \sin(\frac{π}{2}-α)=\cosα \end{eqnarray}
よって、
\begin{eqnarray} {\color{red}{\sin(α-β)=\sinα\cosβ-\cosα\sinβ}}\end{eqnarray}
sin(α+β)の証明
sin(α-β)の、\(\displaystyle {\color{red}{β}}\)を\(\displaystyle {\color{red}{-β}}\)に入れ替える!
\begin{eqnarray} \sin(α+β)=\sinα\cos(-β)-\cosα\sin(-β) \end{eqnarray}
\begin{eqnarray} \cos(-β)=\cosβ \sin(-β)=-\sinβ\end{eqnarray}
よって、
\begin{eqnarray} {\color{red}{\sin(α+β)=\sinα\cosβ+\cosα\sinβ}}\end{eqnarray}
tan(α-β)の証明
\begin{eqnarray} \tan(α-β)=\frac{\sin(α-β)}{\cos(α-β)} \end{eqnarray}
\begin{eqnarray} \tan(α-β) &=& \frac{\sinα\cosβ-\cosα\sinβ}{\cosα\cosβ+\sinα\sinβ} \end{eqnarray}
分母・分子を、\(\displaystyle {\color{red}{\cosα\cosβ}}\)で割る!
\begin{eqnarray} \tan(α-β) &=& \frac{\frac{\sinα}{\cosα}-\frac{\sinβ}{\cosβ}}{1+\frac{\sinα}{\cosα}・\frac{\sinβ}{\cosβ}} \\ &=& \frac{\tanα-\tanβ}{1+\tanα\tanβ}\end{eqnarray}
よって、
\begin{eqnarray} {\color{red}{\tan(α-β)=\frac{\tanα-\tanβ}{1+\tanα\tanβ}}}\end{eqnarray}
tan(α+β)の証明
tan(α-β)の、\(\displaystyle {\color{red}{β}}\)を\(\displaystyle {\color{red}{-β}}\)に入れ替える!
\begin{eqnarray} \tan(α+β) &=& \frac{\tanα-\tan(-β)}{1+\tanα\tan(-β)}\end{eqnarray}
\begin{eqnarray} \tan(-β)=-\tanβ \end{eqnarray}
よって、
\begin{eqnarray} {\color{red}{\tan(α+β)=\frac{\tanα+\tanβ}{1-\tanα\tanβ}}}\end{eqnarray}
暗記?証明?どっちがおすすめ?
結論としては、基本的には暗記をおすすめします!
理由としては、以下が挙げられます!
- 語呂合わせや符号の入れ替えで簡単に覚えられる
- 証明する手間がいらないので、試験中より早く解ける
上のメリットはかなりでかいです!
とは言え、東大で出題されたことがあると考えると、
難関国立大学志望者や個別試験で数学を使う難関私立大学志望者は、
三角関数の仕組みを理解するという点において、証明する方が良いと思います!
まとめ
いかがでしたでしょうか?
加法定理は一見難しそうですが、暗記も証明も簡単にできることが分かったかと思います!
しかし、cos(α-β)以外の導出では、以下の公式も使用しました。
\begin{eqnarray} \tanθ=\frac{\sinθ}{\cosθ}\end{eqnarray}
\begin{eqnarray} \cos(-θ)=\cosθ \sin(-θ)=-\sinθ \tan(-θ)=-\tanθ \end{eqnarray}
\begin{eqnarray} \cos(\frac{π}{2}-θ)=\sinθ \sin(\frac{π}{2}-θ)=\cosθ\end{eqnarray}
加法定理の証明では、以上のような公式も頭に入っていることが前提なので要注意です!
三角関数の公式をまとめて頭に入れるには、sinやcos、tanの仕組みを理解する必要があります!
それについては、別記事で挙げようと思います!
それでは、また!



