第\(\displaystyle 3\)問
袋の中にカードが\(\displaystyle 2\)枚以上入っており、それぞれのカードにはアルファベットが\(\displaystyle 1\)文字だけ書かれている。この箱の中からカードを\(\displaystyle 1\)枚取り出し、書かれているアルファベットを確認してから元に戻すという試行を繰り返し行う。
(1)
箱の中に\(\displaystyle A, B\)のカードが\(\displaystyle 1\)枚ずつ全部で\(\displaystyle 2\)枚入っている場合を考える。以下では、\(\displaystyle 2\)以上の自然数\(\displaystyle n\)に対し、\(\displaystyle n\)回の試行で\(\displaystyle A, B\)がそろっているとは、\(\displaystyle n\)回の試行で\(\displaystyle A, B\)のそれぞれが少なくとも\(\displaystyle 1\)回は取り出されることを意味する。
\(\displaystyle (i)\) \(\displaystyle 2\)回の試行で\(\displaystyle A, B\)がそろっている確率は、
\(\displaystyle 1\)回目:\(\displaystyle A\)、\(\displaystyle 2\)回目:\(\displaystyle B\) \(\displaystyle ⇒\) \(\displaystyle (1\)回目に\(\displaystyle A\)が出る確率)\(\displaystyle \times\)\(\displaystyle (2\)回目に\(\displaystyle B\)が出る確率)\(\displaystyle =\frac{1}{2}\times\frac{1}{2}=\frac{1}{4}\)・・・①
\(\displaystyle 1\)回目:\(\displaystyle B\)、\(\displaystyle 2\)回目:\(\displaystyle A\) \(\displaystyle ⇒\) \(\displaystyle (1\)回目に\(\displaystyle B\)が出る確率)\(\displaystyle \times\)\(\displaystyle (2\)回目に\(\displaystyle A\)が出る確率)\(\displaystyle =\frac{1}{2}\times\frac{1}{2}=\frac{1}{4}\)・・・②
①②より、\(\displaystyle \frac{1}{4}+\frac{1}{4}=\frac{ア:{\color{red}{1}}}{イ:{\color{red}{2}}}\)
\(\displaystyle (ii)\) \(\displaystyle 3\)回の試行で\(\displaystyle A, B\)がそろっている確率を求める。
例えば、\(\displaystyle 3\)回の試行のうち\(\displaystyle A\)を\(\displaystyle 1\)回、\(\displaystyle B\)を\(\displaystyle 2\)回取り出す取り出し方は\(\displaystyle 3\)通り、それらをすべて挙げると次のようになる。
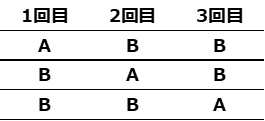
このように考えることにより、\(\displaystyle 3\)回の試行で\(\displaystyle A, B\)がそろっている取り出し方は、\(\displaystyle A⇔B\)を逆にするともう\(\displaystyle 3\)通り考えられるので、
ウ:\(\displaystyle {\color{red}{6}}\)通り
よって、\(\displaystyle 3\)回の試行で\(\displaystyle A, B\)がそろっている確率は、\(\displaystyle\frac{6}{2^{3}}\)
\(\displaystyle (iii)\) \(\displaystyle 4\)回の試行で\(\displaystyle A, B\)がそろっている取り出し方は、
\(\displaystyle 2^{4}\)(全ての場合の数)\(\displaystyle -2\)(4回とも\(\displaystyle A\)あるいは\(\displaystyle B\))\(\displaystyle =\)エオ:\(\displaystyle {\color{red}{14}}\)
よって、\(\displaystyle 4\)回の試行で\(\displaystyle A, B\)がそろっている確率は、
\(\displaystyle \frac{14}{2^{4}}=\frac{カ:{\color{red}{7}}}{キ:{\color{red}{8}}}\)
(2)
箱の中に\(\displaystyle A, B, C\)のカードが\(\displaystyle 1\)枚ずつ全部で\(\displaystyle 3\)枚入っている場合を考える。以下では、\(\displaystyle 3\)以上の自然数\(\displaystyle n\)に対し、\(\displaystyle n\)回目の試行で初めて\(\displaystyle A, B, C\)がそろうとは、\(\displaystyle n\)回の試行で\(\displaystyle A, B, C\)のそれぞれが少なくとも\(\displaystyle 1\)回は取り出され、かつ\(\displaystyle A, B, C\)のうちいずれか\(\displaystyle 1\)枚が\(\displaystyle n\)回目の試行で初めて取り出されることを意味する。
\(\displaystyle (i)\) \(\displaystyle 3\)回目の試行で初めて\(\displaystyle A, B, C\)がそろう取り出し方は、
\(\displaystyle 3!=\)ク:\(\displaystyle {\color{red}{6}}\)通り
よって、\(\displaystyle 3\)回目の試行で初めて\(\displaystyle A, B, C\)がそろう確率は、\(\displaystyle\frac{6}{3^{3}}\)
\(\displaystyle (ii)\) \(\displaystyle 4\)回目の試行で初めて\(\displaystyle A, B, C\)がそろう確率を求める。
\(\displaystyle 4\)回目の試行で初めて\(\displaystyle A, B, C\)がそろう取り出し方は、(1)の(ii)を振り返ることにより、\(\displaystyle 3\times\)(ウ:\(\displaystyle 6\))通りあることが分かる。
よって、\(\displaystyle 4\)回目の試行で初めて\(\displaystyle A, B, C\)がそろう確率は、
\(\displaystyle\frac{3\times6}{3^{4}}=\frac{ケ:{\color{red}{2}}}{コ:{\color{red}{9}}}\)
\(\displaystyle (iii)\) \(\displaystyle 5\)回目の試行で初めて\(\displaystyle A, B, C\)がそろう取り出し方は、
\(\displaystyle 3\times\)(エオ:\(\displaystyle 14\))\(\displaystyle =\)サシ:\(\displaystyle {\color{red}{42}}\)通りある。
よって、\(\displaystyle 5\)回目の試行で初めて\(\displaystyle A, B, C\)がそろう確率は、\(\displaystyle\frac{42}{3^{5}}\)
(3)
箱の中に\(\displaystyle A, B, C\)のカードが\(\displaystyle 1\)枚ずつ全部で\(\displaystyle 4\)枚入っている場合を考える。
以下では、\(\displaystyle 6\)回目の試行で初めて\(\displaystyle A, B, C, D\)がそろうとは、\(\displaystyle 6\)回の試行で\(\displaystyle A, B, C, D\)のそれぞれが少なくとも\(\displaystyle 1\)回は取り出され、かつ\(\displaystyle A, B, C, D\)のうちいずれか\(\displaystyle 1\)枚が\(\displaystyle 6\)回目の試行で初めて取り出されることを意味する。
また、\(\displaystyle 3\)以上\(\displaystyle 5\)以下の自然数\(\displaystyle n\)に対し、\(\displaystyle 6\)回の試行のうち\(\displaystyle n\)回目の試行で初めて\(\displaystyle A, B, C\)だけがそろうとは、\(\displaystyle 6\)回の試行のうち\(\displaystyle 1\)回目から\(\displaystyle n\)回目の試行で\(\displaystyle A, B, C\)のそれぞれが少なくとも\(\displaystyle 1\)回は取り出され、\(\displaystyle D\)は\(\displaystyle 1\)回も取り出されず、かつ\(\displaystyle A, B, C\)のうちいずれか\(\displaystyle 1\)枚が\(\displaystyle n\)回目の試行で初めて取り出されることを意味する。\(\displaystyle 6\)回の試行のうち\(\displaystyle n\)回目の試行で初めて\(\displaystyle B, C, D\)だけがそろうなども同様に定める。
太郎さんと花子さんは、\(\displaystyle 6\)回目の試行で初めて\(\displaystyle A, B, C, D\)がそろう確率について考えている。
太郎:例えば、\(\displaystyle 5\)回目までに\(\displaystyle A, B, C\)のそれぞれが少なくとも\(\displaystyle 1\)回は取り出され、かつ\(\displaystyle 6\)回目に初めて\(\displaystyle D\)が取り出される場合を考えたら計算できそうだね。
花子:それなら、初めて\(\displaystyle A, B, C\)だけがそろうのが、\(\displaystyle 3\)回目のとき、\(\displaystyle 4\)回目のとき、\(\displaystyle 5\)回目のときで分けて考えてみてはどうかな。
\(\displaystyle 3\)回目のとき、
\(\displaystyle 3\)回目の試行で初めて\(\displaystyle A, B, C\)がそろう取り出し方は、ク:\(\displaystyle 6\)通り
よって、「\(\displaystyle 3\)回目の試行で初めて\(\displaystyle A, B, C\)がそろい、かつ\(\displaystyle 6\)回目の試行で初めて\(\displaystyle D\)が取り出される」取り出し方は、
\(\displaystyle 6\times3\times3\times1=\)スセ:\(\displaystyle {\color{red}{54}}\)・・・①
\(\displaystyle 4\)回目のとき、
「\(\displaystyle 4\)回目の試行で初めて\(\displaystyle A, B, C\)がそろい、かつ\(\displaystyle 6\)回目の試行で初めて\(\displaystyle D\)が取り出される」取り出し方は、
\(\displaystyle (3\times6)\times3\times1=\)ソタ:\(\displaystyle {\color{red}{54}}\)・・・②
\(\displaystyle 5\)回目のとき、
「\(\displaystyle 5\)回目の試行で初めて\(\displaystyle A, B, C\)がそろい、かつ\(\displaystyle 6\)回目の試行で初めて\(\displaystyle D\)が取り出される」取り出し方は、
(サシ:\(\displaystyle 42)\times1=42\)・・・③
①②③より、\(\displaystyle 54+54+42=150\)
「初めて\(\displaystyle D\)が取り出される」だけでなく、「初めて\(\displaystyle A, B, C\)が取り出される」パターンもあるので、
\(\displaystyle 150\times4=600\)
よって、\(\displaystyle 6\)回目の試行で初めて\(\displaystyle A, B, C, D\)がそろう確率は、
\(\displaystyle \frac{600}{4^{6}}=\frac{チツ:{\color{red}{75}}}{テトナ:{\color{red}{512}}}\)


