問題
\(\displaystyle (1)\) \(\displaystyle 2\)次方程式\(\displaystyle x^{2}+2x-4=0\)の解を\(\displaystyle α, β\)とするとき、\(\displaystyle α-\frac{1}{α}, β-\frac{1}{β}\)を解にもつ\(\displaystyle 2\)次方程式は
\(\displaystyle x^{2}+\frac{{\color{red}{(1)(2)}}}{{\color{red}{(3)(4)}}}x+\frac{{\color{red}{(5)(6)}}}{{\color{red}{(7)(8)}}}=0\)
である。また、\(\displaystyle α^{2}-\frac{1}{α^{2}}, β^{2}-\frac{1}{β^{2}}\)を解にもつ\(\displaystyle 2\)次方程式は
\(\displaystyle x^{2}+\frac{{\color{red}{(9)(10)(11)}}}{{\color{red}{(12)(13)(14)}}}x+\frac{{\color{red}{(15)(16)(17)}}}{{\color{red}{(18)(19)(20)}}}=0\)
である。
\(\displaystyle (2)\) \(\displaystyle 10\)の階乗\(\displaystyle 10!=1\times2\times・・・\times10\)を計算すると\(\displaystyle 3628800\)であり、下の桁から\(\displaystyle 2\)個の\(\displaystyle 0\)が続く。同じ
ように、\(\displaystyle 20\)の階乗\(\displaystyle 20!\)は下の桁から\(\displaystyle {\color{red}{(21)(22)}}\)個の\(\displaystyle 0\)が続く数、\(\displaystyle 100\)の階乗\(\displaystyle 100!\)は下の桁から\(\displaystyle {\color{red}{(23)(24)}}\)個
の\(\displaystyle 0\)が続く数、\(\displaystyle 2024\)の階乗\(\displaystyle 2024!\)は下の桁から\(\displaystyle {\color{red}{(25)(26)(27)}}\)個の\(\displaystyle 0\)が続く数となる。
負でない実数\(\displaystyle t\)に対して定義される関数
\(\displaystyle f(t)=\frac{9}{2}t-3\int_0^1 \left|(x-t)(x-2t)\right|dx\)
を\(\displaystyle t\)の範囲に応じて多項式で書くと
\(\displaystyle (a)0\text{≦}t<\frac{{\color{red}{(28)(29)}}}{{\color{red}{(30)(31)}}}\)において
\(\displaystyle f(t)={\color{red}{(32)(33)}}t^{3}+{\color{red}{(34)(35)}}t^{2}+{\color{red}{(36)(37)}}t+{\color{red}{(38)(39)}}\)
\(\displaystyle (b)\frac{{\color{red}{(28)(29)}}}{{\color{red}{(30)(31)}}}\text{≦}t<{\color{red}{(40)(41)}}\)において
\(\displaystyle f(t)={\color{red}{(42)(43)}}t^{3}+{\color{red}{(44)(45)}}t^{2}+{\color{red}{(46)(47)}}\)
\(\displaystyle (c){\color{red}{(40)(41)}}\text{≦}t\)において
\(\displaystyle f(t)={\color{red}{(48)(49)}}t^{2}+{\color{red}{(50)(51)}}t+{\color{red}{(52)(53)}}\)
である。よって\(\displaystyle t=\frac{{\color{red}{(54)(55)}}}{{\color{red}{(56)(57)}}}\)のとき、\(\displaystyle f(t)\)は最大値\(\displaystyle \frac{{\color{red}{(58)(59)}}}{{\color{red}{(60)(61)}}}\)をとる。
スポーツなどの競技では、コイントスによって試合の先攻と後攻を決めることがある。通常、コイントスではコインの表と裏は等確率\(\displaystyle \frac{1}{2}\)で出ると仮定するが、異なる確率で表と裏が出るコインを考えることもできる。いま、\(\displaystyle 3:2\)の比で表と裏が出るコインと\(\displaystyle 2:3\)の比で表と裏が出るコインの\(\displaystyle 2\)枚がある状況を考える。
\(\displaystyle (1)\) どちらか\(\displaystyle 1\)枚のコインを無作為に選んでコイントスを行うとき、表が出る確率は\(\displaystyle \frac{{\color{red}{(62)(63)}}}{{\color{red}{(64)(65)}}}\)である。
\(\displaystyle (2)\) どちらか\(\displaystyle 1\)枚のコインを無作為に選んでコイントスを行ったところ、表が出た。このコインを使ってもう\(\displaystyle 1\)回コイントスを行うとき、表が出る確率は\(\displaystyle \frac{{\color{red}{(66)(67)}}}{{\color{red}{(68)(69)}}}\)である。
\(\displaystyle (3)\) どちらか\(\displaystyle 1\)枚のコインを無作為に選んで\(\displaystyle 2\)回コイントスを行ったところ、\(\displaystyle 2\)回とも表が出た。このコインを使ってもう\(\displaystyle 1\)回コイントスを行うとき、表が出る確率は\(\displaystyle \frac{{\color{red}{(70)(71)}}}{{\color{red}{(72)(73)}}}\)である。
\(\displaystyle (4)\) \(\displaystyle 2\)枚のコインを使って同時にコイントスを行うとき、両方のコインの表裏が同じになる確率は\(\displaystyle \frac{{\color{red}{(74)(75)}}}{{\color{red}{(76)(77)}}}\)である。
\(\displaystyle (5)\) \(\displaystyle 2\)枚のコインを使って同時にコイントスを行ったところ、一方のコインは表、もう一方のコインは裏が出た。表が出たコインを使ってもう\(\displaystyle 1\)回コイントスを行うとき、表が出る確率は\(\displaystyle \frac{{\color{red}{(78)(79)}}}{{\color{red}{(80)(81)}}}\)である。

点\(\displaystyle O\)を中心とする半径\(\displaystyle 2\)の球から点\(\displaystyle O\)を中心とする半径\(\displaystyle r\)(\(\displaystyle r\)は\(\displaystyle 0<r<2\)を満たす実数)の球をくり抜いてできた立体\(\displaystyle V\)がある。いま、点\(\displaystyle O\)から下ろした垂線の長さが\(\displaystyle x\)(\(\displaystyle x\)は\(\displaystyle 0<x<2\)を満たす実数)である平面\(\displaystyle P\)で立体\(\displaystyle V\)を切り、\(\displaystyle 2\)つの立体に分ける。\(\displaystyle 2\)つの立体のうち、体積の小さい方を\(\displaystyle V_{1},\)大きい方を\(\displaystyle V_{2}\)とする。
\(\displaystyle (1)\) 平面\(\displaystyle P\)による立体\(\displaystyle V\)の切り口の面積が\(\displaystyle π(2-r)^{2}\)であるとき、\(\displaystyle x=\sqrt{{\color{red}{(82)(83)}}r^{2}+{\color{red}{(84)(85)}}r}\)である。
\(\displaystyle (2)\) \(\displaystyle 0<x<r\)のとき、\(\displaystyle V_{1}\)の体積は
\(\displaystyle (r^{2}+{\color{red}{(86)(87)}})πx+\frac{{\color{red}{(88)(89)}}}{{\color{red}{(90)(91)}}}πr^{3}+\frac{{\color{red}{(92)(93)}}}{{\color{red}{(94)(95)}}}π\)
であり、\(\displaystyle r\text{≦}x<2\)のとき、\(\displaystyle V_{1}\)の体積は
\(\displaystyle \frac{{\color{red}{(96)(97)}}}{{\color{red}{(98)(99)}}}πx^{3}+{\color{red}{(100)(101)}}πx+\frac{{\color{red}{(102)(103)}}}{{\color{red}{(104)(105)}}}π\)
である。
\(\displaystyle (3)\) \(\displaystyle x=r\)において\(\displaystyle V_{1}\)の体積と\(\displaystyle V_{2}\)の体積の比が\(\displaystyle 1:3\)になるとき、\(\displaystyle r={\color{red}{(106)(107)}}+\sqrt{{\color{red}{(108)(109)}}}\)である。また、\(\displaystyle x=\frac{2}{3}r\)において\(\displaystyle V_{1}\)の体積と\(\displaystyle V_{2}\)の体積の比が\(\displaystyle 1:3\)になるとき、\(\displaystyle r={\color{red}{(110)(111)}}+\sqrt{{\color{red}{(112)(113)}}}\)である。
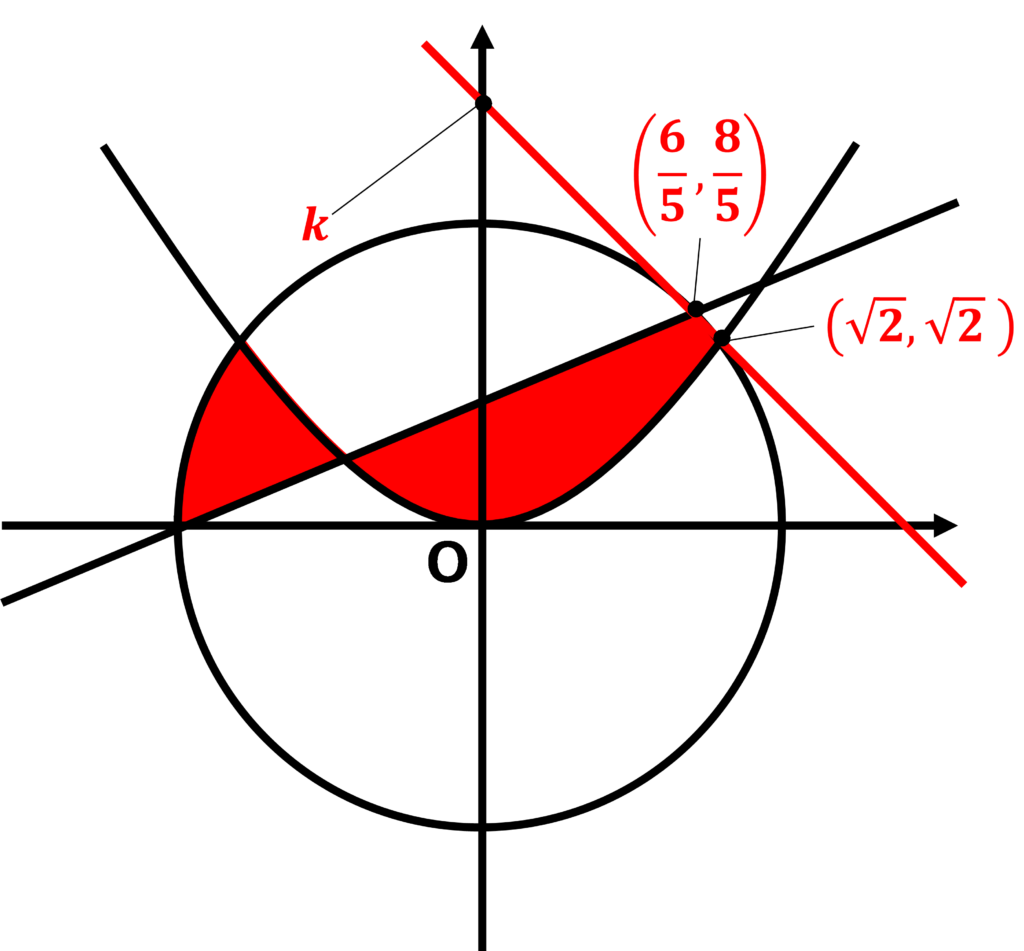
実数\(\displaystyle x, y\)について、次の連立不等式があらわす領域を\(\displaystyle D\)とする。
\(\displaystyle \begin{eqnarray} \left\{ \begin{array}{l} x^{2}+y^{2}\text{≦}4 \\ (\sqrt{2}x^{2}-2y)(x-2y+2)\text{≦}0 \end{array} \right. \end{eqnarray}\)
点\(\displaystyle (x,y)\)が領域\(\displaystyle D\)を動くとき
\(\displaystyle (1)\) \(\displaystyle x-2y\)は
点\(\displaystyle \left(\frac{{\color{red}{(114)(115)}}}{{\color{red}{(116)(117)}}}\sqrt{2},\frac{{\color{red}{(118)(119)}}}{{\color{red}{(120)(121)}}}\sqrt{2}\right)\)において最大値\(\displaystyle \frac{{\color{red}{(122)(123)}}}{{\color{red}{(124)(125)}}}\sqrt{2}\)
点\(\displaystyle ({\color{red}{(126)(127)}}\sqrt{2},{\color{red}{(128)(129)}}\sqrt{2})\)において最小値\(\displaystyle {\color{red}{(130)(131)}}\sqrt{2}\)
をとる。
\(\displaystyle (2)\) \(\displaystyle ax+y\)が点\(\displaystyle \left(\frac{6}{5},\frac{8}{5}\right)\)で最大となるような実数\(\displaystyle a\)のとりうる値の範囲は
\(\displaystyle {\color{red}{(132)(133)}}+{\color{red}{(134)(135)}}\sqrt{2}\text{≦}a\text{≦}\frac{{\color{red}{(136)(137)}}}{{\color{red}{(138)(139)}}}\)
であり、この条件下で\(\displaystyle ax+y\)のとりうる値の範囲は
\(\displaystyle {\color{red}{(140)(141)}}+{\color{red}{(142)(143)}}\sqrt{2}\text{≦}ax+y\text{≦}\frac{{\color{red}{(144)(145)}}}{{\color{red}{(146)(147)}}}\)
である。
解答
\(\displaystyle 2\)次方程式\(\displaystyle x^{2}+2x-4=0\)の解が、\(\displaystyle α,β\)であることから、
\(\displaystyle x^{2}+2x-4=0\)
\(\displaystyle →x^{2}-(α+β)x+αβ=0\)
・・・①
よって、\(\displaystyle α-\frac{1}{α},β-\frac{1}{β}\)を解にもつ\(\displaystyle 2\)次方程式は以下のように表せる。
\(\displaystyle x^{2}-\{{\color{red}{(α-\frac{1}{α})+(β-\frac{1}{β})}}\}x\)
\(\displaystyle +{\color{blue}{(α-\frac{1}{α})(β-\frac{1}{β})}}=0\)
赤と青の値をそれぞれ求める!
①より、\(\displaystyle α+β=-2,αβ=-4\)であるため、
\(\displaystyle {\color{red}{(α-\frac{1}{α})+(β-\frac{1}{β})}}\)
\(\displaystyle =(α+β)-(\frac{1}{α}+\frac{1}{β})\)
\(\displaystyle ={\color{red}{-\frac{5}{2}}}\)
\(\displaystyle {\color{blue}{(α-\frac{1}{α})(β-\frac{1}{β})}}\)
\(\displaystyle =αβ-\frac{α}{β}-\frac{β}{α}+\frac{1}{αβ}\)
\(\displaystyle ={\color{blue}{-\frac{5}{4}}}\)
したがって、
同様に、\(\displaystyle α^{2}-\frac{1}{α^{2}},β^{2}-\frac{1}{β^{2}}\)を解にもつ\(\displaystyle 2\)次方程式は以下のように表せる。
\(\displaystyle x^{2}-\{{\color{red}{(α^{2}-\frac{1}{α^{2}})+(β^{2}-\frac{1}{β^{2}})}}\}x\)
\(\displaystyle +{\color{blue}{(α^{2}-\frac{1}{α^{2}})(β^{2}-\frac{1}{β^{2}})}}=0\)
赤と青の値をそれぞれ求める!
①より、\(\displaystyle α+β=-2,αβ=-4\)であるため、
\(\displaystyle {\color{red}{(α^{2}-\frac{1}{α^{2}})+(β^{2}-\frac{1}{β^{2}})}}\)
\(\displaystyle =(α^{2}+β^{2})-(\frac{1}{α^{2}}+\frac{1}{β^{2}})\)
\(\displaystyle ={\color{red}{\frac{45}{4}}}\)
\(\displaystyle {\color{blue}{(α^{2}-\frac{1}{α^{2}})(β^{2}-\frac{1}{β^{2}})}}\)
\(\displaystyle =α^{2}β^{2}-\frac{α^{2}}{β^{2}}-\frac{β^{2}}{α^{2}}+\frac{1}{α^{2}β^{2}}\)
\(\displaystyle =\color{blue}{\frac{145}{16}}\)
したがって、
\(\displaystyle 🔲!\)の下桁の0の数は、\(\displaystyle 🔲\div{\color{red}{5}}\)
\(\displaystyle 20!\)の場合、\(\displaystyle 20\div5={\color{red}{4}}\)
\(\displaystyle 🔲\)の範囲が、\(\displaystyle {\color{red}{5^{n}}}\text{≦}🔲<{\color{red}{5^{n+1}}}(n\text{≧}3)\)のとき、\(\displaystyle 🔲\div{\color{red}{5}}+🔲\div{\color{red}{5^{2}}}+・・・\)
\(\displaystyle +🔲\div{\color{red}{5^{n}}}\)
\(\displaystyle 100!\)の場合、\(\displaystyle 100\div5+100\div5^{2}={\color{red}{24}}\)
割り算の計算結果は、切り捨て!
Ex) \(\displaystyle 2024\div5={\color{red}{404}}\)あまり \(\displaystyle 4\)
\(\displaystyle 2024!\)の場合、
\(\displaystyle 2024\div5+2024\div5^{2}+2024\div5^{3}\)
\(\displaystyle +2024\div5^{4}\)
\(\displaystyle =404+80+16+3\)
\(\displaystyle ={\color{red}{503}}\)
\(\displaystyle \int\)の範囲である\(\displaystyle 0\)と\(\displaystyle 1\)、その間の\(\displaystyle \frac{1}{2}\)、そして\(\displaystyle t\)の大小によって、\(\displaystyle f(t)\)の値が変わる!
\(\displaystyle (a) 0\text{≦}t<\frac{1}{2}\)のとき、
\(\displaystyle f(t)=\frac{9}{2}t-3\int_0^1 \left|(x-t)(x-2t)\right|dx\)
\(\displaystyle =-t^{3}-6t^{2}+9t-1\)
\(\displaystyle (b) \frac{1}{2}\text{≦}t<1\)のとき、
\(\displaystyle f(t)=\frac{9}{2}t-3\int_0^1 \left|(x-t)(x-2t)\right|dx\)
\(\displaystyle =-5t^{3}+6t^{2}+1\)
\(\displaystyle (c) 1\text{≦}t\)のとき、
\(\displaystyle f(t)=\frac{9}{2}t-3\int_0^1 \left|(x-t)(x-2t)\right|dx\)
\(\displaystyle =-6t^{2}+9t-1\)
\(\displaystyle t\)の範囲ごとの、\(\displaystyle y=f(t)\)のグラフの形を考える!
\(\displaystyle 0\text{≦}t<\frac{1}{2}\)のとき、
\(\displaystyle f(t)=-t^{3}-6t^{2}+9t-1\)
\(\displaystyle f'(t)=-3t^{2}-12t+9=-3(t+2)^{2}\)
\(\displaystyle +21{\color{red}{>0}}\)
\(\displaystyle f'(t)>0\)より、\(\displaystyle f(t)\)は増加し続ける!・・・①
\(\displaystyle \frac{1}{2}\text{≦}t<1\)のとき、
\(\displaystyle f(t)=-5t^{3}+6t^{2}+1\)
\(\displaystyle f'(t)=-15t^{2}+12t=-3t(5t-4)\)
\(\displaystyle f'(t)=0\)のとき、\(\displaystyle t=0,\frac{4}{5}\)なので、
\(\displaystyle t=\frac{4}{5}\)で極大値\(\displaystyle f\left(\frac{4}{5}\right)=\frac{57}{25}\)・・・②
\(\displaystyle 1\text{≦}t\)のとき、
\(\displaystyle f(t)=-6t^{2}+9t-1\)
\(\displaystyle f'(t)=-12t+9{\color{red}{<0}}\)
\(\displaystyle f'(t)<0\)より、\(\displaystyle f(t)\)は減少し続ける!・・・③
①②③より、\(\displaystyle y=f(t)\)を図示すると次のようになる。
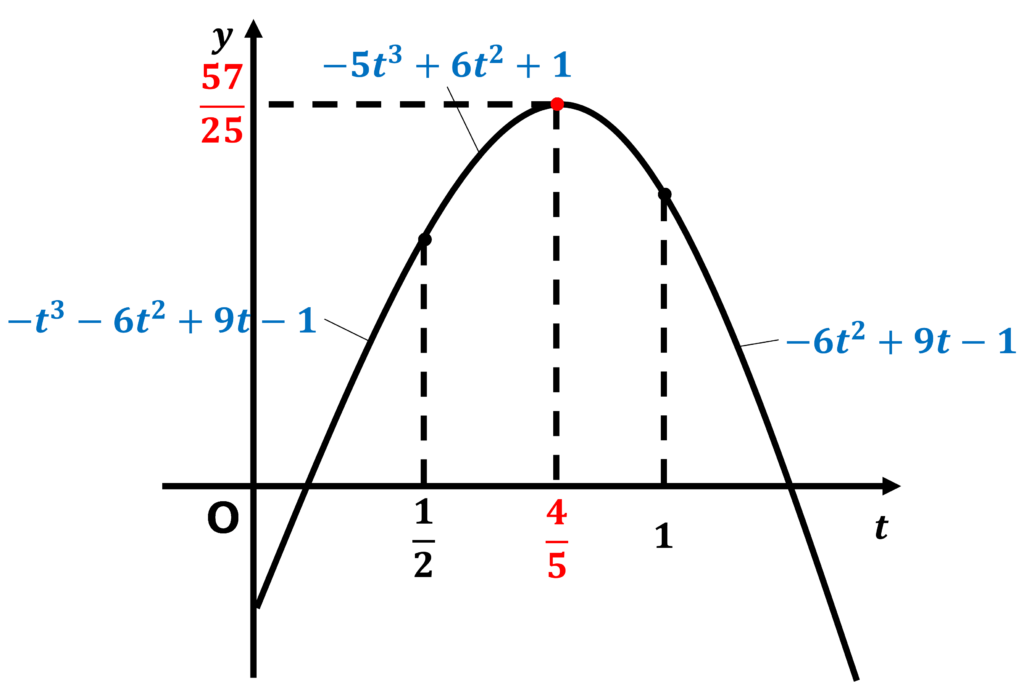
よって、
事象 \(\displaystyle A\) \(\displaystyle 3:2\)の比で表と裏が出るコインを選ぶ
事象 \(\displaystyle B\) \(\displaystyle 2:3\)の比で表と裏が出るコインを選ぶ
事象 \(\displaystyle S\) コイントスを\(\displaystyle 1\)回行い、表が出る
事象 \(\displaystyle T\) コイントスを\(\displaystyle 1\)回行い、裏が出る
\(\displaystyle P(A)P_{A}(S)+P(B)P_{B}(S)=\frac{1}{2}・\frac{3}{5}+\frac{1}{2}・\frac{2}{5}={\color{red}{\frac{1}{2}}}\)
「表が出た。」というところで文章が2分割されていることから、条件付き確率を使う!
(i)「表が出た。」までの確率は以下である。
\(\displaystyle P(A)P_{A}(S)+P(B)P_{B}(S)=\frac{1}{2}・\frac{3}{5}+\frac{1}{2}・\frac{2}{5}=\frac{1}{2}\)・・・①
(ii)「もう\(\displaystyle 1\)回コイントスを行う」までの確率は以下である。
\(\displaystyle P(A)P_{A}(S){\color{red}{P_{A}(S)}}+P(B)P_{B}(S){\color{red}{P_{B}(S)}}\)
\(\displaystyle =\frac{1}{2}・\frac{3}{5}・{\color{red}{\frac{3}{5}}}+\frac{1}{2}・\frac{2}{5}・{\color{red}{\frac{2}{5}}}\)
\(\displaystyle =\frac{13}{50}\)・・・②
\(\displaystyle ②\div①\)より、
\(\displaystyle \frac{13}{50}\div\frac{1}{2}={\color{red}{\frac{13}{25}}}\)
「表が出た。」というところで文章が2分割されていることから、条件付き確率を使う!
(i)「表が出た。」までの確率は以下である。
\(\displaystyle P(A)P_{A}(S)P_{A}(S)+P(B)P_{B}(S)P_{B}(S)\)
\(\displaystyle =\frac{1}{2}・\frac{3}{5}・\frac{3}{5}+\frac{1}{2}・\frac{2}{5}・\frac{2}{5}\)
\(\displaystyle =\frac{13}{50}\)・・・①
(ii)「もう\(\displaystyle 1\)回コイントスを行う」までの確率は以下である。
\(\displaystyle P(A)P_{A}(S)P_{A}(S){\color{red}{P_{A}(S)}}\)
\(\displaystyle +P(B)P_{B}(S)P_{B}(S){\color{red}{P_{B}(S)}}\)
\(\displaystyle =\frac{1}{2}・\frac{3}{5}・\frac{3}{5}・{\color{red}{\frac{3}{5}}}+\frac{1}{2}・\frac{2}{5}・\frac{2}{5}・{\color{red}{\frac{2}{5}}}\)
\(\displaystyle =\frac{7}{50}\)・・・②
\(\displaystyle ②\div①\)より、
\(\displaystyle \frac{7}{50}\div\frac{13}{50}={\color{red}{\frac{7}{13}}}\)
\(\displaystyle \frac{3}{5}・\frac{2}{5}+\frac{2}{5}・\frac{3}{5}={\color{red}{\frac{12}{25}}}\)
「裏が出た。」というところで文章が2分割されていることから、条件付き確率を使う!
(i)「裏が出た。」までの確率は以下である。
\(\displaystyle \frac{3}{5}・\frac{3}{5}+\frac{2}{5}・\frac{2}{5}=\frac{13}{25}\)・・・①
(ii)「もう\(\displaystyle 1\)回コイントスを行う」までの確率は以下である。
\(\displaystyle \frac{3}{5}・\frac{3}{5}・{\color{red}{\frac{3}{5}}}+\frac{2}{5}・\frac{2}{5}・{\color{red}{\frac{2}{5}}}=\frac{7}{25}\)・・・②
\(\displaystyle ②\div①\)より、
\(\displaystyle \frac{7}{25}\div\frac{13}{25}={\color{red}{\frac{7}{13}}}\)
\(\displaystyle x\)と\(\displaystyle r\)の大小によって、切り口の面積が異なる!
(ⅰ) \(\displaystyle 0<x<r\)のとき、

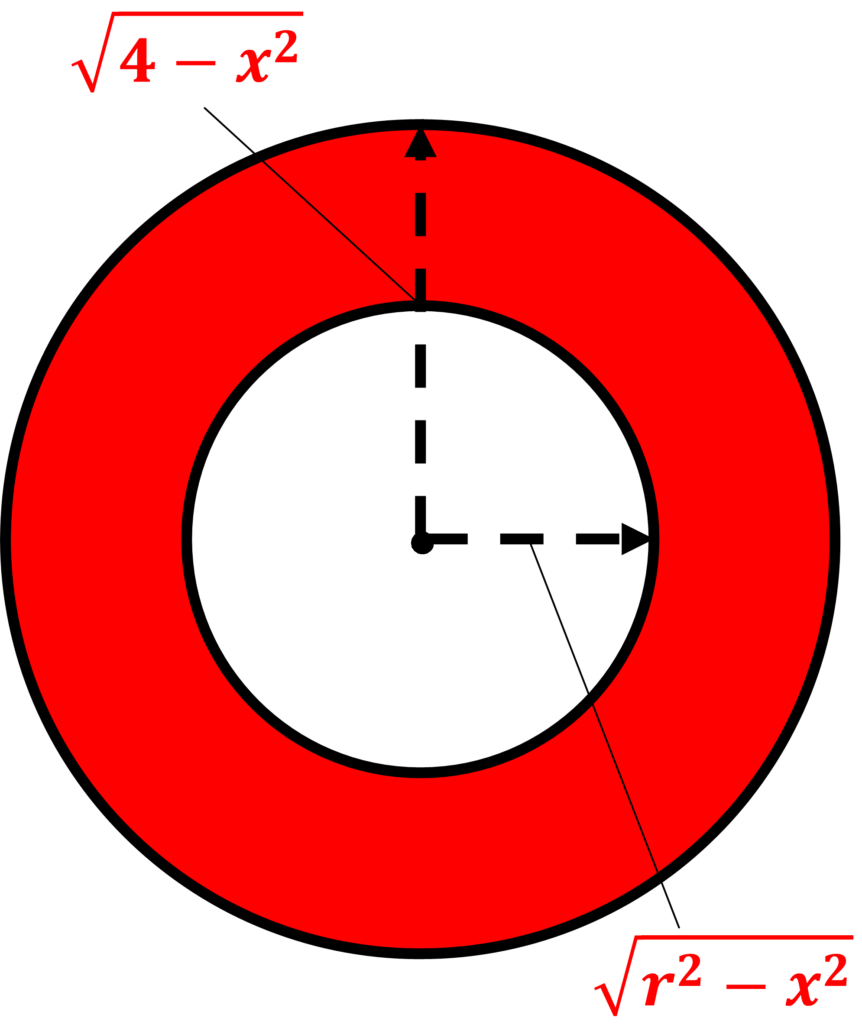
\(\displaystyle π(\sqrt{4-x^{2}})^{2}-π(\sqrt{r^{2}-x^{2}})^{2}\)
\(\displaystyle =π\{(4-x^{2})-(r^{2}-x^{2})\}\)
\(\displaystyle =π(4-r^{2})\)・・・①
(ⅱ) \(\displaystyle r\text{≦}x<2\)のとき、
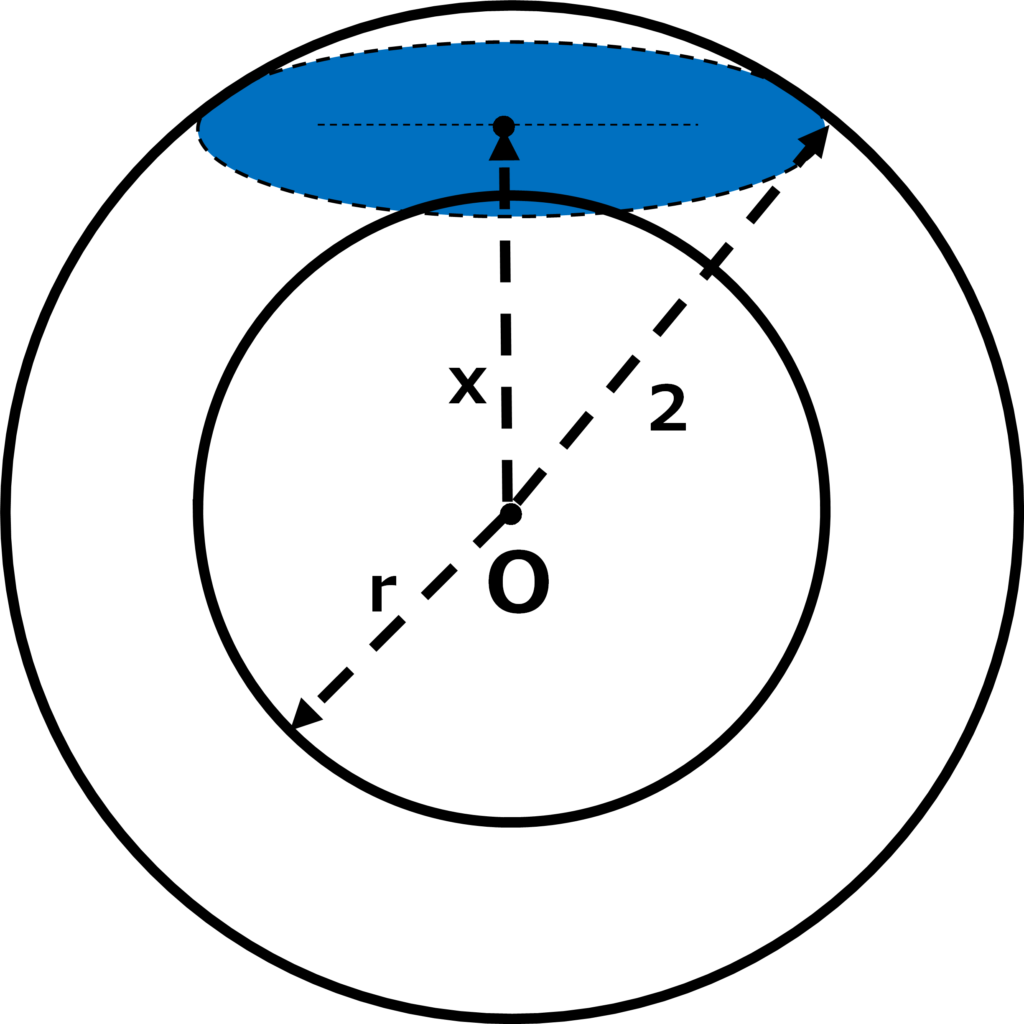
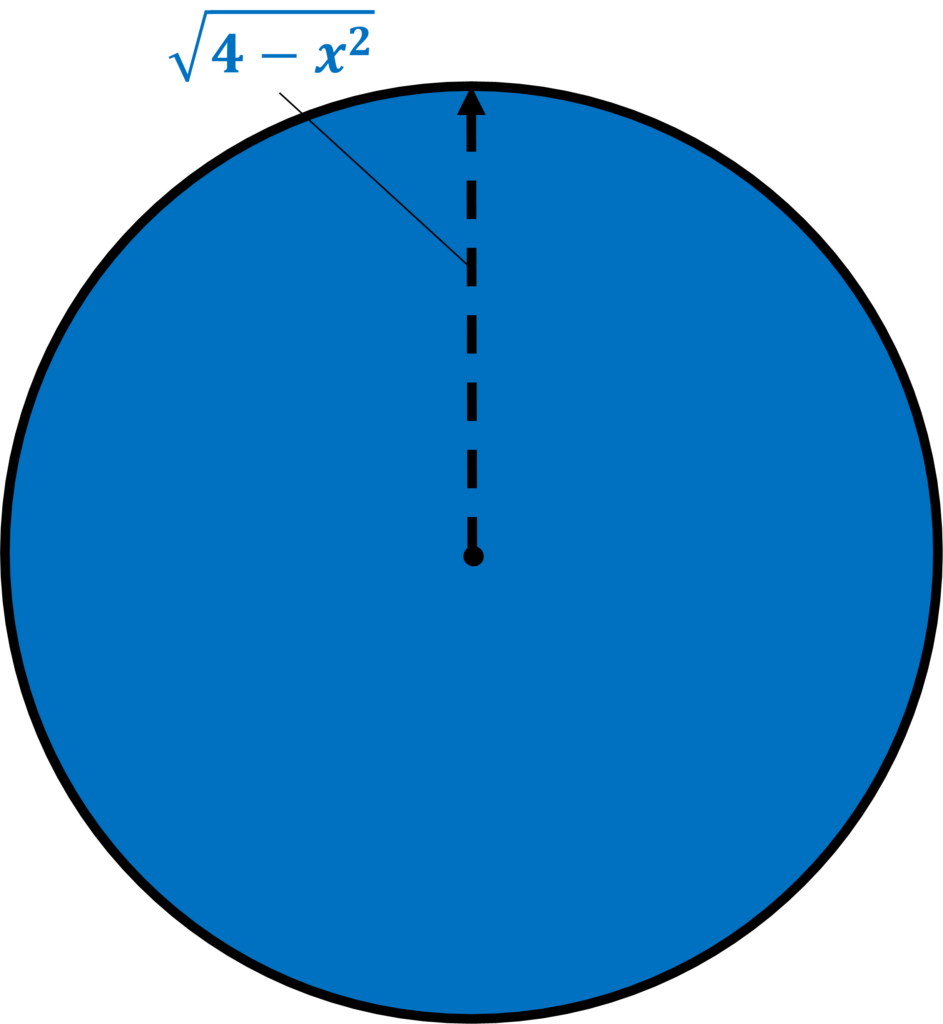
\(\displaystyle π(\sqrt{4-x^{2}})^{2}=π(4-x^{2})\)・・・②
\(\displaystyle ①=π(2-r)^{2}, ②=π(2-r)^{2}\)の方程式を作り、\(\displaystyle x=?\)を求める!
(ⅲ) \(\displaystyle ①=π(2-r)^{2}\)のとき、
\(\displaystyle π(4-r^{2})=π(2-r)^{2}\)
式に\(\displaystyle x\)がないので不可
(ⅳ) \(\displaystyle ②=π(2-r)^{2}\)のとき、
\(\displaystyle π(4-x^{2})=π(2-r)^{2}\)
\(\displaystyle 4-x^{2}=(2-r)^{2}\)
\(\displaystyle x^{2}=4-(2-r)^{2}=4-(4-4r+r^{2})=4r-r^{2}\)
\(\displaystyle V_{1}\)の体積を\(\displaystyle T_{1}\)とする。
\(\displaystyle x\)と\(\displaystyle r\)の大小によって、体積が異なる!
(ⅰ) \(\displaystyle 0<x<r\)のとき、
\(\displaystyle T_{1}=\int_x^r π(4-r^{2})dx+\int_r^2 π(4-x^{2})dx\)
\(\displaystyle =(r^{2}-4)πx-\frac{2}{3}πr^{3}+\frac{16}{3}π\)
(ⅱ) \(\displaystyle r\text{≦}x<2\)のとき、
\(\displaystyle T_{1}=\int_x^2 π(4-x^{2})dx=\frac{1}{3}πx^{3}-4πx+\frac{16}{3}π\)
\(\displaystyle V_{2}\)の体積を\(\displaystyle T_{2}\)とする。
\(\displaystyle T_{1}:T_{2}=1:3\)⇒\(\displaystyle T_{1}:T_{1}+T_{2}=1:4\)
\(\displaystyle x=r\)のとき、
(2)の解答より、\(\displaystyle T_{1}=\frac{1}{3}πr^{3}-4πr+\frac{16}{3}π\)・・・①
\(\displaystyle T_{1}+T_{2}\)は立体\(\displaystyle V\)を表しているため、
\(\displaystyle T_{1}+T_{2}=\frac{4}{3}π(2^{3}-r^{3})\)・・・②
①、②より、
\(\displaystyle \frac{1}{3}πr^{3}-4πr+\frac{16}{3}π:\frac{4}{3}π(2^{3}-r^{3})=1:4\)
\(\displaystyle (r-2)(r^{2}+2r-2)=0\)
\(\displaystyle 0<r<2\)より、\(\displaystyle r=-1+\sqrt{3}\)
\(\displaystyle x=\frac{2}{3}r\)のとき、
\(\displaystyle T_{1}=-\frac{8}{3}πr+\frac{16}{3}π\)・・・③
②、③より、
\(\displaystyle -\frac{8}{3}πr+\frac{16}{3}π:\frac{4}{3}π(2^{3}-r^{3})=1:4\)
\(\displaystyle (r-2)(r^{2}+2r-4)=0\)
\(\displaystyle 0<r<2\)より、\(\displaystyle r=-1+\sqrt{5}\)
\(\displaystyle \begin{eqnarray} \left\{ \begin{array}{l} {\color{red}{x^{2}+y^{2}\text{≦}4}} \\ (\sqrt{2}x^{2}-2y)(x-2y+2)\text{≦}0 \\ ⇒{\color{red}{\frac{1}{2}x+1\text{≦}y\text{≦}\frac{\sqrt{2}}{2}x^{2}}} or {\color{red}{\frac{\sqrt{2}}{2}x^{2}\text{≦}y\text{≦}\frac{1}{2}x+1}} \end{array} \right. \end{eqnarray}\)
図にすると、以下のようになる。

\(\displaystyle x-2y=k\)とする。
\(\displaystyle x-2y=k\)⇒\(\displaystyle y=\frac{1}{2}x-\frac{1}{2}k\)が、網目にぎりぎり接するときの\(\displaystyle k\)の最大値と最小値を考える!
切片\(\displaystyle -\frac{1}{2}k\)は負であるため、直線が上にあるほど、\(\displaystyle k\)は小さくなる。
\(\displaystyle k\)が最小値のとき、\(\displaystyle y=\frac{1}{2}x-\frac{1}{2}k\)は以下の図のように通る。
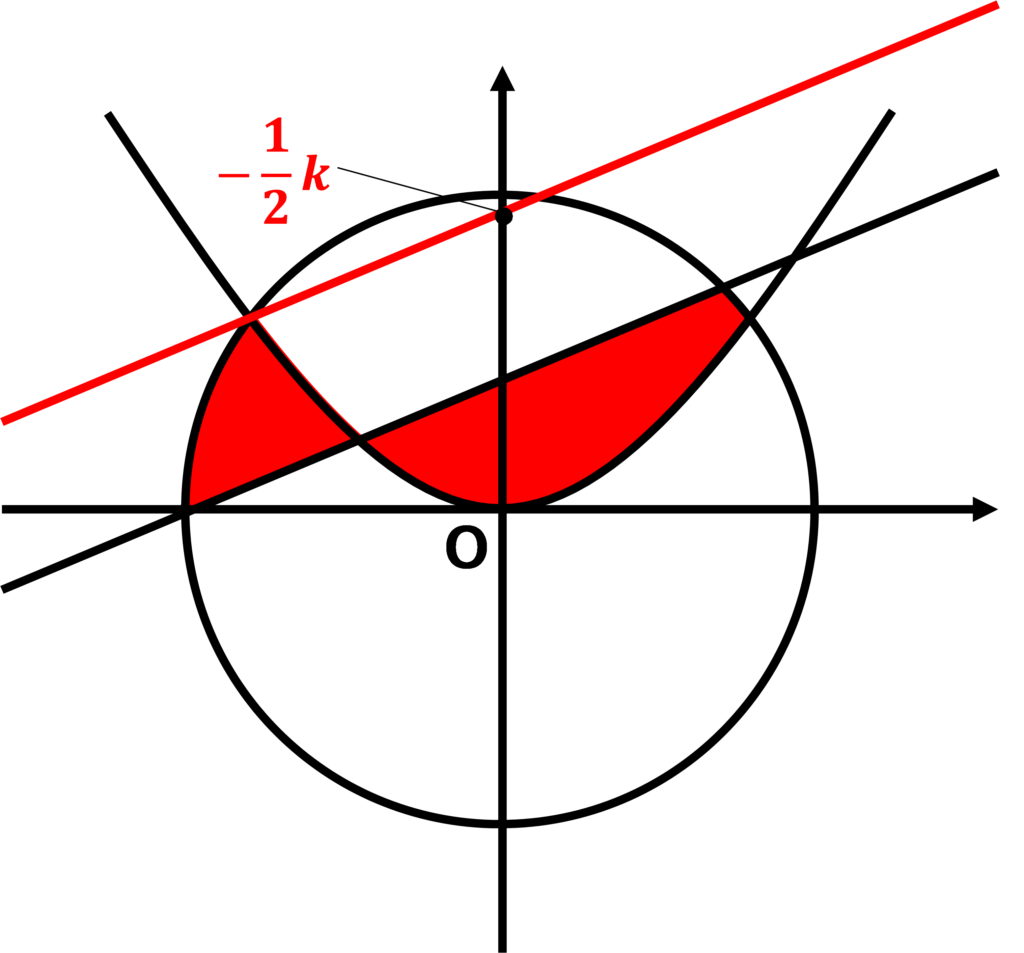
このとき、\(\displaystyle y=\frac{1}{2}x-\frac{1}{2}k\)は、
円\(\displaystyle x^{2}+y^{2}=4\)と直線\(\displaystyle y=\frac{\sqrt{2}}{2}x^{2}\)の交点を通る。
\(\displaystyle \begin{eqnarray} \left\{ \begin{array}{l} x^{2}+y^{2}=4 \\ y=\frac{\sqrt{2}}{2}x^{2} \end{array} \right. \end{eqnarray}\)
\(\displaystyle \frac{2}{\sqrt{2}}y+y^{2}=4⇒y^{2}+\sqrt{2}y-4=0\)
\(\displaystyle y=\frac{-\sqrt{2}\pm\sqrt{(\sqrt{2})^{2}-4・(-4)}}{2}=\frac{-\sqrt{2}\pm3\sqrt{2}}{2}=\sqrt{2}, -\sqrt{2}\)
上図より、\(\displaystyle y=\sqrt{2}\)・・・①
これを、\(\displaystyle y=\frac{\sqrt{2}}{2}x^{2}\)に代入する。
\(\displaystyle \sqrt{2}=\frac{\sqrt{2}}{2}x^{2}⇒x^{2}=2\)
上図より、\(\displaystyle x=-\sqrt{2}\)・・・②
①、②より、\(\displaystyle k=-\sqrt{2}-2\sqrt{2}={\color{red}{-3\sqrt{2}}}\)
よって、
\(\displaystyle k\)が最大値のとき、\(\displaystyle y=\frac{1}{2}x-\frac{1}{2}k\)は以下の図のように通る。
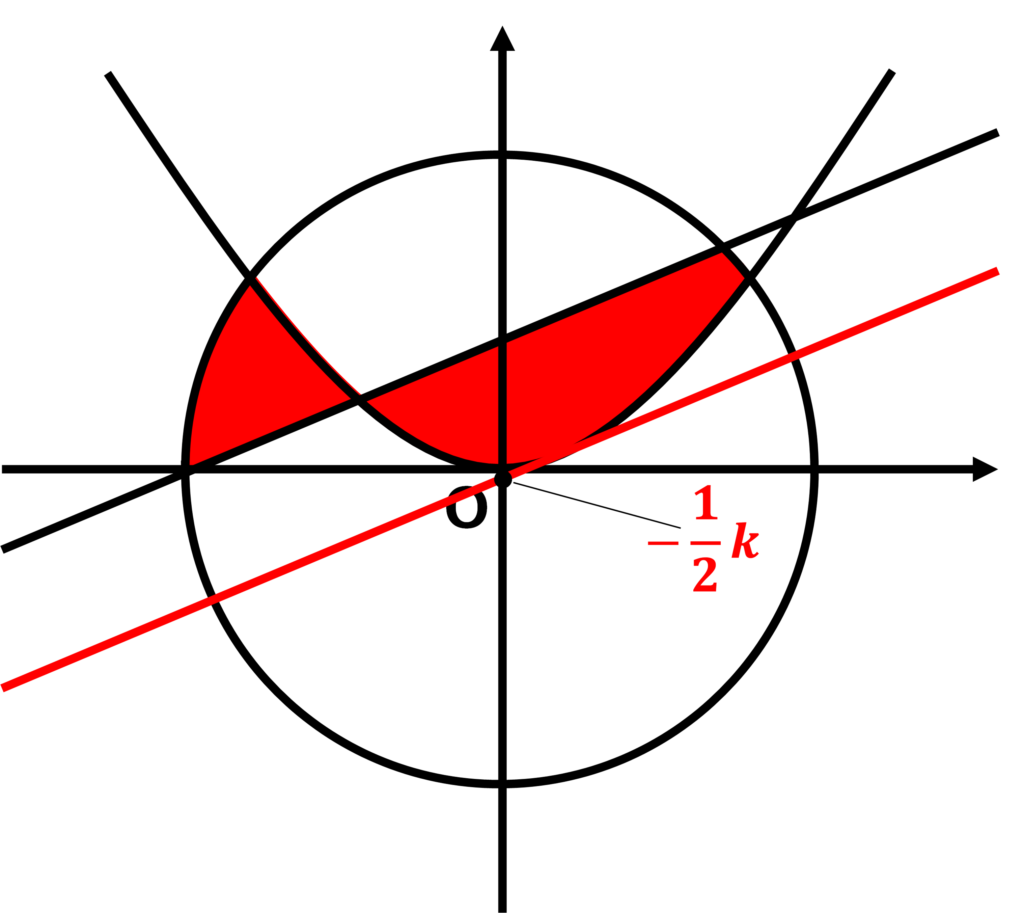
このとき、\(\displaystyle y=\frac{1}{2}x-\frac{1}{2}k\)は、
直線\(\displaystyle y=\frac{\sqrt{2}}{2}x^{2}\)と接する。
\(\displaystyle y=\frac{1}{2}x-\frac{1}{2}k\)と\(\displaystyle y=\frac{\sqrt{2}}{2}x^{2}\)を連立したときの解が、1個になれば良い!
\(\displaystyle \begin{eqnarray} \left\{ \begin{array}{l} y=\frac{1}{2}x-\frac{1}{2}k \\ y=\frac{\sqrt{2}}{2}x^{2} \end{array} \right. \end{eqnarray}\)
\(\displaystyle \frac{\sqrt{2}}{2}x^{2}=\frac{1}{2}x-\frac{1}{2}k\)
\(\displaystyle \sqrt{2}x^{2}-x+k=0\)
\(\displaystyle \sqrt{2}x^{2}-x+k=0\)の判別式\(\displaystyle D=0\)になれば良い!
\(\displaystyle D=1-4\sqrt{2}k=0\)
よって、\(\displaystyle k={\color{red}{\frac{\sqrt{2}}{8}}}\)
このとき、\(\displaystyle \sqrt{2}x^{2}-x+\frac{\sqrt{2}}{8}=0\)
\(\displaystyle 8\sqrt{2}x^{2}-8x+\sqrt{2}=0\)
\(\displaystyle x=\frac{4\pm\sqrt{(-4)^{2}-8\sqrt{2}・\sqrt{2}}}{8\sqrt{2}}=\frac{4}{8\sqrt{2}}=\)\(\displaystyle \frac{\sqrt{2}}{4}\)
また、\(\displaystyle y=\frac{\sqrt{2}}{2}・\left(\frac{\sqrt{2}}{4}\right)^{2}=\frac{\sqrt{2}}{2}・\frac{1}{8}=\)\(\displaystyle \frac{\sqrt{2}}{16}\)
よって、
\(\displaystyle ax+y=k\)とする。
\(\displaystyle ax+y=k\)⇒\(\displaystyle y=-ax+k\)が\(\displaystyle \left(\frac{6}{5}, \frac{8}{5}\right)\)を通り、網目部分にぎりぎり接するときの傾き\(\displaystyle -a\)の値を考える!
\(\displaystyle \left(\frac{6}{5}, \frac{8}{5}\right)\)は、\(\displaystyle x^{2}+y^{2}=4\)と\(\displaystyle y=\frac{1}{2}x+1\)の交点である!
\(\displaystyle -a\)が最大値のとき、\(\displaystyle y=-ax+k\)は以下の図のように通る。
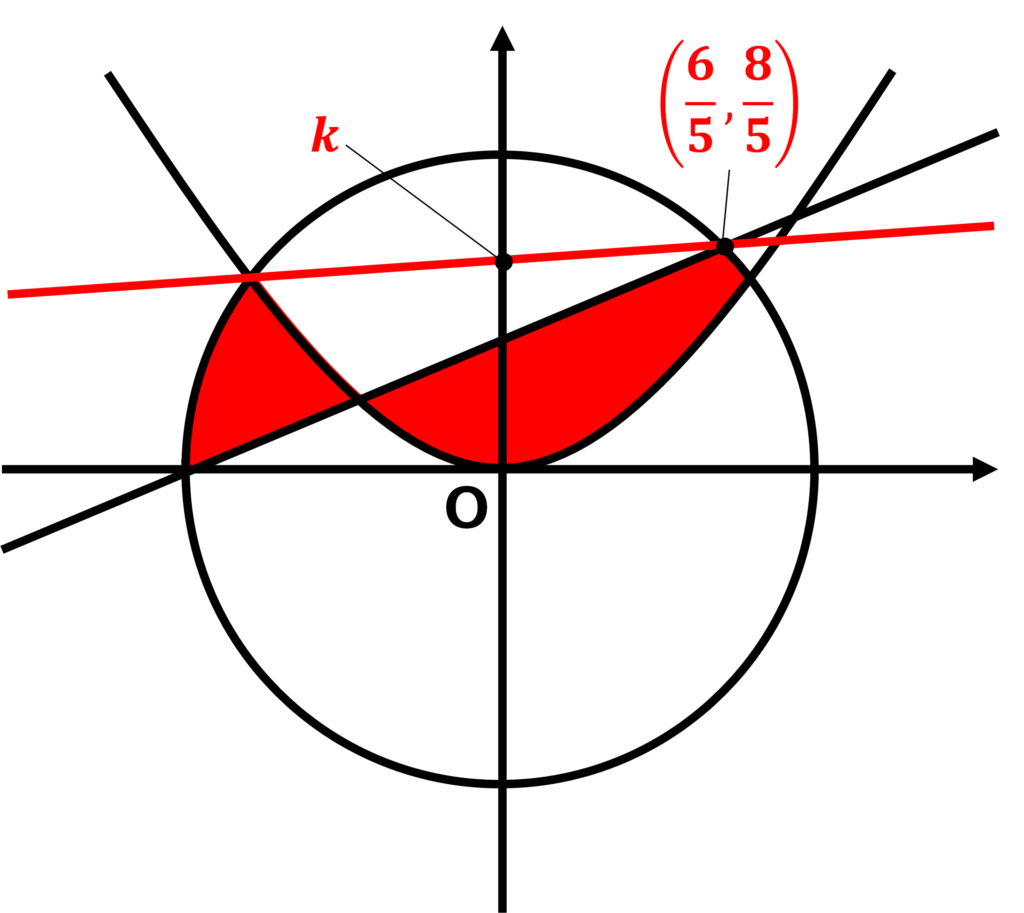
\(\displaystyle x^{2}+y^{2}=4\)と\(\displaystyle y=\frac{\sqrt{2}}{2}x^{2}\)の交点の1つ、
\(\displaystyle (-\sqrt{2}, \sqrt{2})\)を通るため、
\(\displaystyle -a=\left(\frac{8}{5}-\sqrt{2}\right)\div\left(\frac{6}{5}+\sqrt{2}\right)\)
\(\displaystyle =\left(\frac{8}{5}-\sqrt{2}\right)\left(\sqrt{2}-\frac{6}{5}\right)\div\frac{14}{25}=5\sqrt{2}-7\)
よって、\(\displaystyle -a\)が最大値のとき、\(\displaystyle a=7-5\sqrt{2}\)・・・①
\(\displaystyle -a\)が最小値のとき、\(\displaystyle y=-ax+k\)は以下の図のように通る。
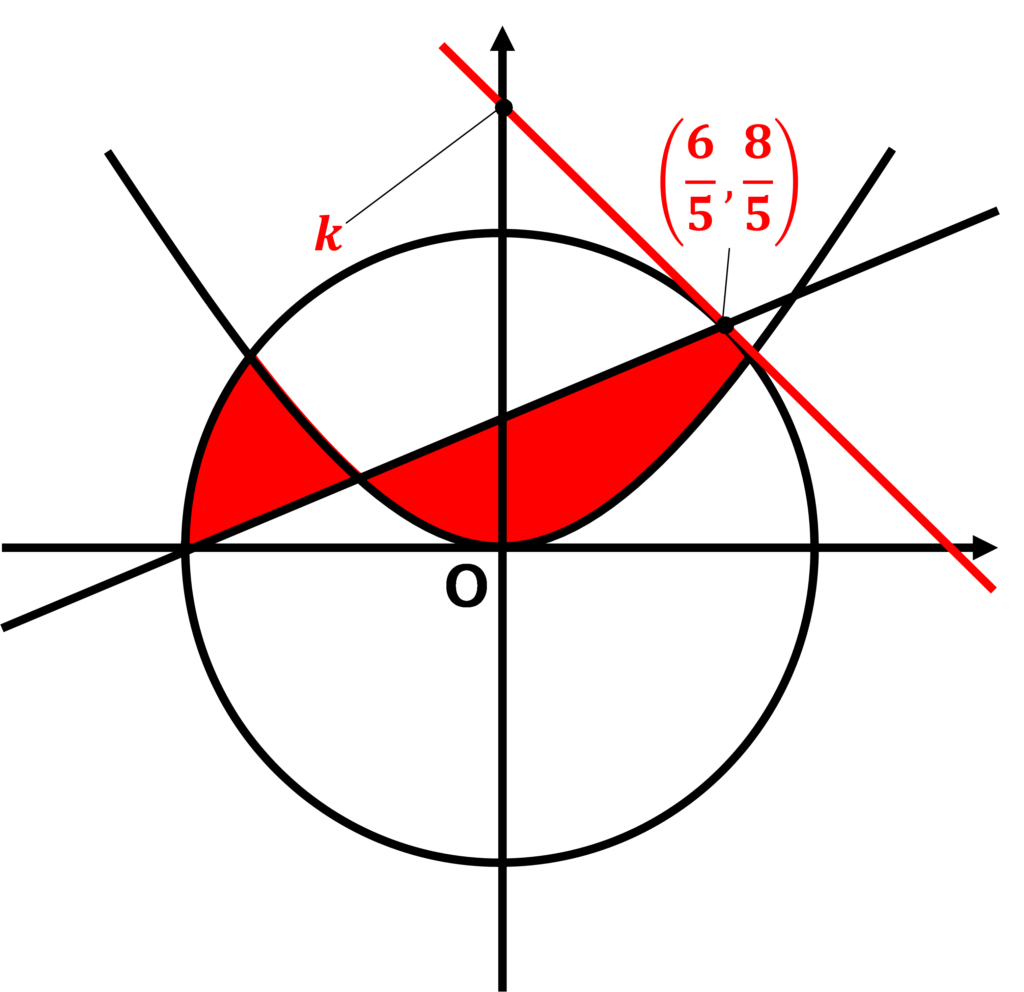
\(\displaystyle x^{2}+y^{2}=4\)において点\(\displaystyle \left(\frac{6}{5}, \frac{8}{5}\right)\)で接している。
接線の方程式は、
\(\displaystyle \frac{6}{5}x+\frac{8}{5}y=4\)
\(\displaystyle y=-\frac{3}{4}x+\frac{5}{2}\)
よって、\(\displaystyle -a\)のが最小値のとき、\(\displaystyle a=\frac{3}{4}\)・・・②
①、②より、
そして、\(\displaystyle ax+y\)の取り得る範囲は、
\(\displaystyle 7-5\sqrt{2}\text{≦}a\text{≦}\frac{3}{4}\)
\(\displaystyle (7-5\sqrt{2})x+y\text{≦}ax+y\text{≦}\frac{3}{4}x+y\)
\(\displaystyle 10-6\sqrt{2}\text{≦}ax+y\text{≦}\frac{5}{2}\)