(1) ある仕事をAさんとBさんの2人ですると10日、Cさんが1人ですると15日かかります。この仕事をAさん、Bさん、Cさんの3人ですると何日かかりますか。
全ての仕事量を1とする。
AさんとBさんの1日の仕事量は、\(\displaystyle\frac{1}{10}\)
Cさんの1日の仕事量は、\(\displaystyle\frac{1}{15}\)
Aさん、Bさん、Cさんの1日の仕事量は、
\(\displaystyle\frac{1}{10}+\frac{1}{15}=\frac{3}{30}+\frac{2}{30}=\frac{5}{30}=\frac{1}{6}\)
分母の数を取って、答えは6日
(2) 下の図は、中心角が90°のおうぎ形です。水色部分の面積は何\(cm^{2}\)ですか。
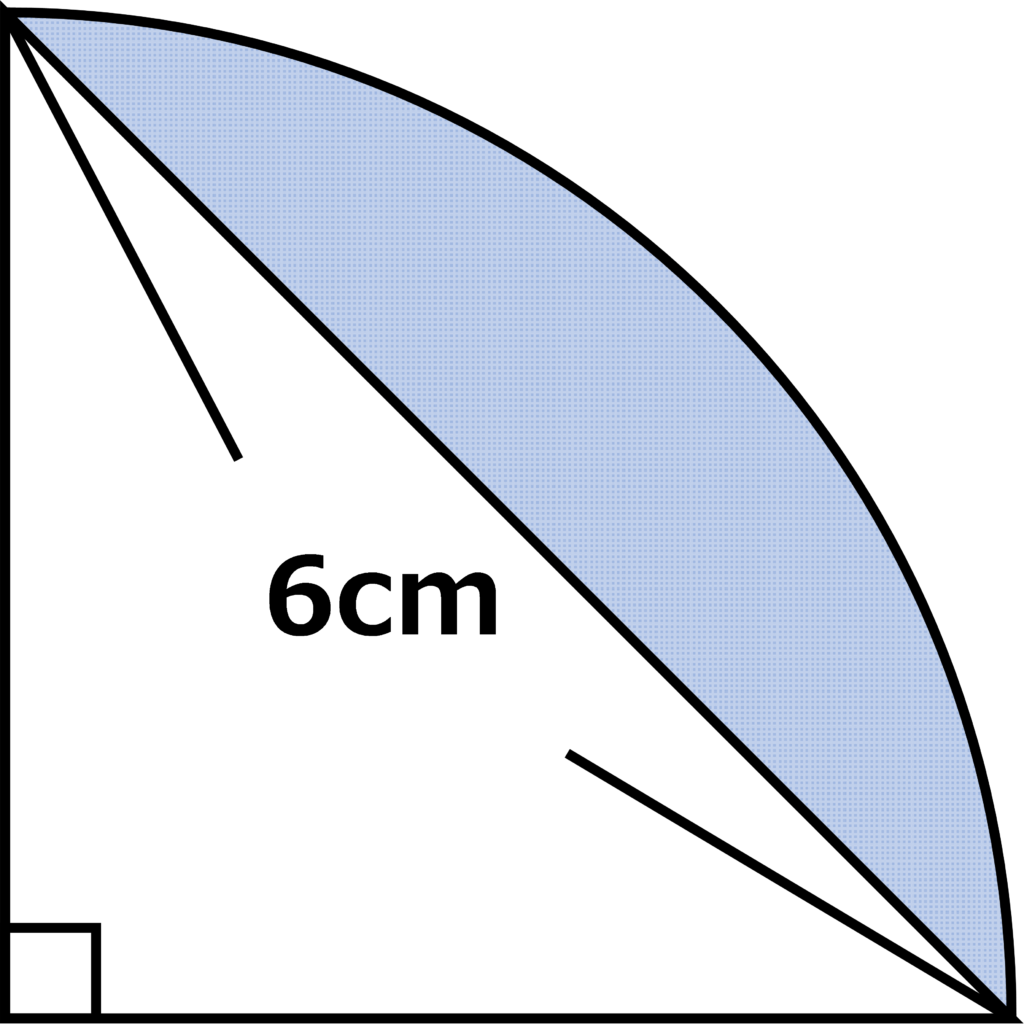
おうぎ形の半径を□cmとする。
おうぎ形の面積は、\((□\times□\times3.14\div4)cm^{2}\)
水色部分以外の直角二等辺三角形の面積は、\((□\times□\div2)cm^{2}\)
水色部分の面積は、上の2つの式を引けば良いので、
\(\displaystyle□\times□\times3.14\div4-□\times□\div2\)
\(\displaystyle□\times□\times\frac{3.14}{4}-□\times□\times\frac{1}{2}\)
\(\displaystyle□\times□\times(\frac{3.14}{4}-\frac{1}{2})\)
\(\displaystyle□\times□\times\frac{1.14}{4}\)・・・①
\(\displaystyle□\times□\)の値が分からない!
そこで、上の直角二等辺三角形において、三平方の定理により、
\(\displaystyle□\times□+□\times□=6\times6\)
\(\displaystyle□\times□\times2=36\)
\(\displaystyle□\times□=18\)・・・②
②の式を、①の\(\displaystyle□\times□\)に入れる。
\(\displaystyle18\times\frac{1.14}{4}\)
\(\displaystyle18\times1.14\div4=\)
(3) 3%の食塩水200gと6%の食塩水を何g混ぜ合わせると4%の食塩水になりますか。
6%の食塩水を□gとする。
\(\displaystyle\frac{3}{100}\times200+\frac{6}{100}\times□=\frac{4}{100}\times(200+□)\)
\(\displaystyle6+\frac{6}{100}\times□=\frac{4}{100}\times□+8\)
\(\displaystyle\frac{6}{100}\times□-\frac{4}{100}\times□=8-6\)
\(\displaystyle\frac{2}{100}\times□=2\)
\(\displaystyle□=\color{red}{100g}\)
(4) 10円玉、50円玉、100円玉を使って210円とする方法は全部で何通りありますか。ただし、使わない硬貨があってもよいものとします。
(i) 10円玉を使う場合
(10×21)
(ii) 50円玉を使う場合
(50×4+10)(50×3+10×6)(50×2+10×11)(50×2+100+10)(50+10×16)(50+100+10×6)
(iii) 100円玉を使う場合
(100×2+10)(100+10×11)
\(\displaystyle1+6+2=\color{red}{9通り}\)
(5) 現在、父の年れいは42才、2人の子どもの年れいは7才と5才です。2人の子どもの年れいの合計が父の年れいの半分になるのは今から何年後ですか。
答えを□年後とする。
\(\displaystyle42+□=2\times\{(7+□)+(5+□)\}\)
\(\displaystyle42+□=2\times(12+□\times2)\)
\(\displaystyle42+□=24+□\times4\)
\(\displaystyle□\times3=18\)
\(\displaystyle□=\color{red}{6年後}\)
(6) はじめ、兄と妹の所持金の比は2:1でした。2人とも母親から500円ずつもらったので、所持金の比は5:3になりました。はじめ、兄はいくら持っていましたか。
兄のはじめの所持金を□円とする。
妹のはじめの所持金は、\(\displaystyle□\times\frac{1}{2}\)
500円ずつもらった時の各々の所持金は5:3なので、
\(\displaystyle□+500:□\times\frac{1}{2}+500=5:3\)
\(\displaystyle3\times(□+500)=5\times(□\times\frac{1}{2}+500)\)
\(\displaystyle□\times3+1500=□\times\frac{5}{2}+2500\)
\(\displaystyle□\times3-□\times\frac{5}{2}=2500-1500\)
\(\displaystyle□\times\frac{1}{2}=1000\)
\(\displaystyle□=\color{red}{2000円}\)


