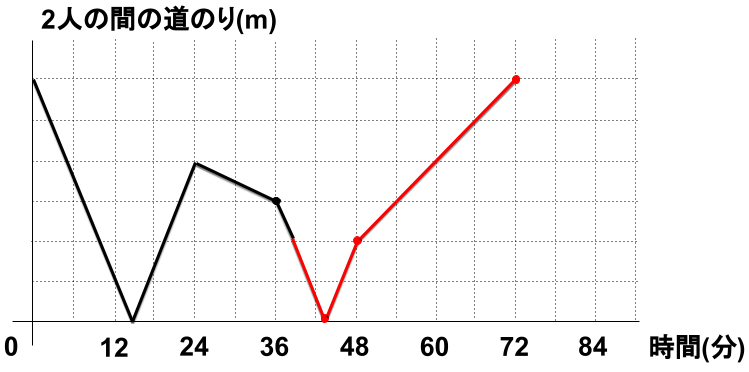
太郎君と花子さんの2人は、それぞれ自宅から相手の家までの道のりを一定の速さで1往復します。太郎君は分速120mで走り、花子さんは太郎君より遅い速さで走ります。2人は同時に自宅を出発しました。次のグラフは、2人の間の道のりの様子を途中まで表したものです。
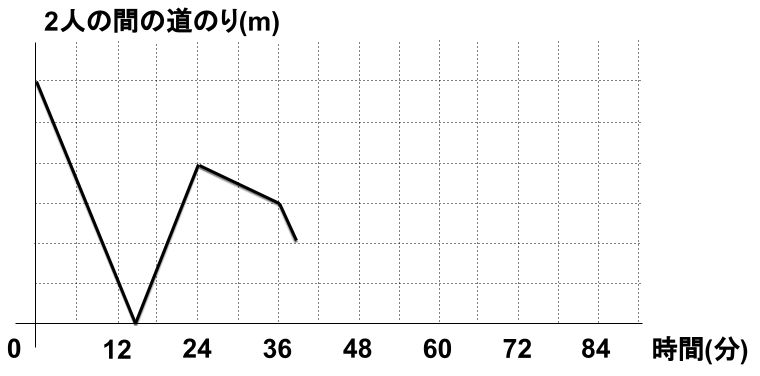
[前準備]
まず、傾きがそれぞれ異なる4本の線のときの、太郎くん・花子さんの道のりを考える。
まとめると、以下になる。
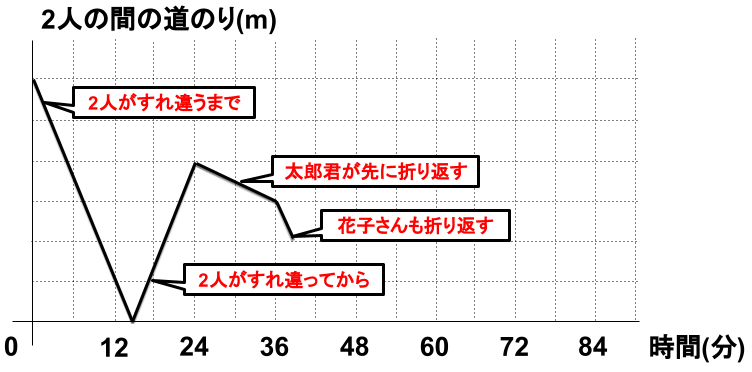
左から1本目→太郎君・花子さんは互いに接近。2人の間の道のりは一気に小さくなる。
左から2本目→太郎君・花子さんは互いに離れる。2人の間の道のりは一気に大きくなる。
左から3本目→足の速い太郎くんが先に折り返す。2人の間の道のりは少し小さくなる。
左から4本目→花子さんも折り返し、再び2人は互いに接近。2人の間の道のりは一気に小さくなる。
(1) 太郎君の家と花子さんの家の間の道のりは何mか、求めなさい。

上図の赤点のところで、太郎君が先に到着している。
この地点で、太郎君は分速120mで24分間走っているため、
\(\displaystyle120\times24=\)2880m
(2) 花子さんの走る速さは、分速何mか、求めなさい。
花子さんが折り返し始めるのは、36分。
(1)の問題から、2人の家の間の道のりは2880mであるため、
\(\displaystyle2880\div36=\)分速80m
(3) 太郎君と花子さんが2回目に出会ったのは、出発して何分何秒後か、求めなさい。
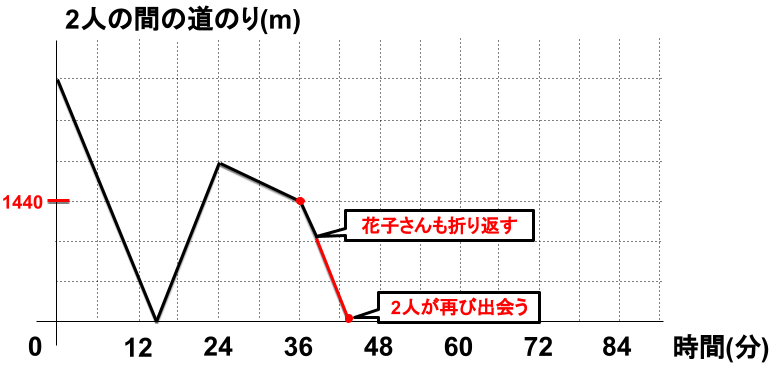
36分時点の2人の間の道のりは、上図のように1440m。
また、花子さんも折り返すため、2人は1分間に200m(分速120m+分速80m)ずつ接近していく。
そのため、計算式は以下のようになる。
\(\displaystyle1440\div200=7.2分\)
7.2分は、7分+0.2分であり、0.2分を秒数に直す。
\(\displaystyle0.2分=0.2分\times60秒=12秒\)
最後に、36分に7分と12秒を足すと、
43分12秒後
(4) 花子さんが走り終わるまでのグラフを完成させなさい。
まず、(3)の43分12秒の位置まで、線を伸ばす。
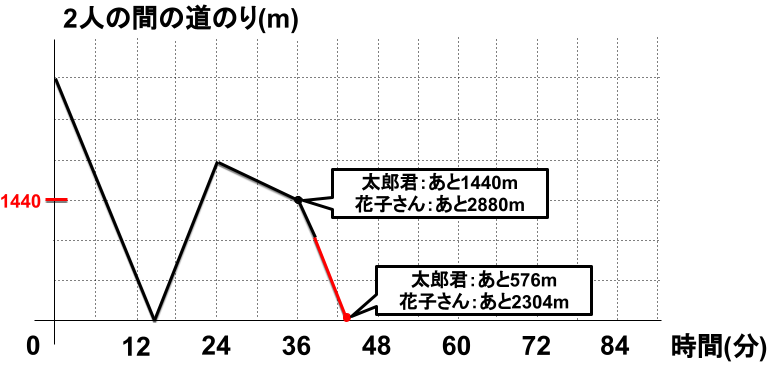
上図は、36分と43分12秒時点の、2人の往復し終えるまでの残りの道のりを表したものである。
ちなみに、43分12秒時点の2人の残りの道のりは、以下のように計算する。
\(\displaystyle1440m-分速120\times7.2分=576m\)
\(\displaystyle2880m-分速80\times7.2分=2304m\)
次に、太郎君が到着するまでを線で結ぶ。
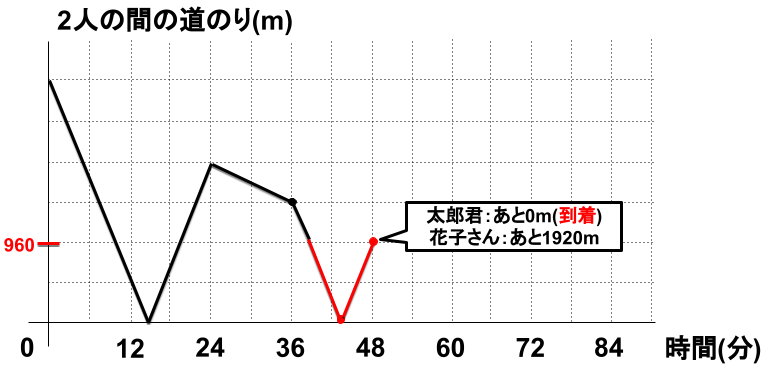
太郎君の到着時点での道のりは960m、時間は48分である。
太郎君の残りの576mは分速120m進むので、時間は、
\(\displaystyle576\div120=4.8分 43.2分(43分12秒)+4.8分=48分\)
4.8分間に、2人は1分に200mずつ離れていくので、2人の間の道のりは、
\(4.8\times200=960m\)
最後に、花子さんは残りの1920mを分速80mで走るので、
\(1920\div80=24分\)
そのため、72分後(48分+24分)に元の位置に戻るため、正解は以下のグラフになる。