3点A, B, Cそれぞれを中心とする半径2cmの円があります。図のように3つの円がすべて1点Pを通るとき、次の問いに答えなさい。

(1) 三角形ABCが正三角形となるとき、3つの円を解答欄に作図しなさい。

手順①:点Pを中心とする半径2cmの円を描く!
手順②:・円の周上に点Aを取る(どこでもいい)!
・点Aと点Pを結ぶ!
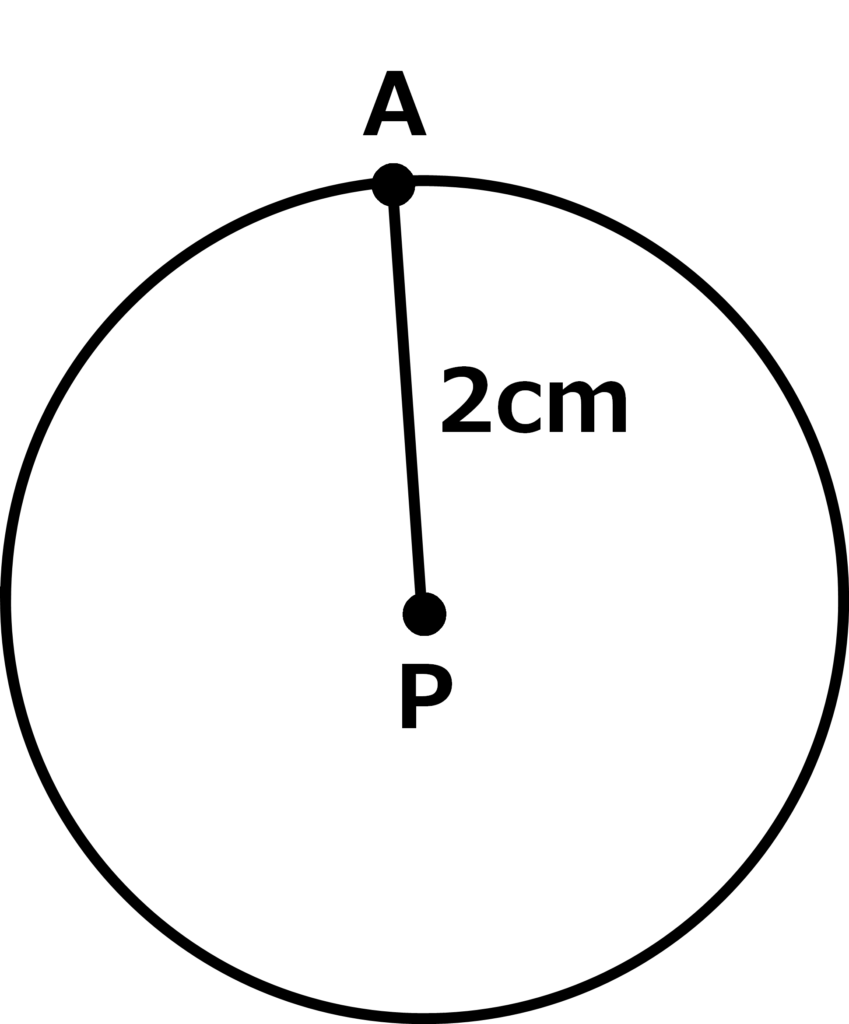
手順③:・点Aを始点として、左右に30°ずつ測る!
・それぞれの線と円との交点を点B, Cとする!

手順④:点Pを通るようにして、点A, B, Cを中心とする円を描く!
答え↓

(2) (1)で作成した図形の周の長さを求めなさい。
3つの円周(A, B, C)の合計は、
\(\displaystyle(2+2)\times3.14\times3\)
\(\displaystyle=4\times3.14\times3\)
\(\displaystyle=12\times3.14\)
\(\displaystyle=37.68\)・・・①
ただ、周の長さに含まれない円の部分もある!(下図の青い円の内側の部分)

含まれない部分は、ちょうど半径2cm1個分にあたる!
\(\displaystyle(2+2)\times3.14\)
\(\displaystyle=4\times3.14\)
\(\displaystyle=12.56\)・・・②
①-②より、
\(\displaystyle37.68-12.56=\color{red}{25.12cm}\)


