※当ブログは、「文系数学受験生」を対象としているため、数Ⅲに関わる知識を披露しかねることをあらかじめご了承ください。
数Ⅲの知識はないものの、それ以外の数学分野は全身全霊でサポートしたいので、今後ともよろしくお願いいたします。
みなさん、数学Aで習う「内分と外分」をご存じでしょうか?
「内分」は、ある線分を線上の任意の点で分けることで、
「外分」は、ある線分を線外の任意の点で分けることを意味します!

そしたら「内分点」には、中点とかも含まれてるんだね!

そうだね、ただ中点以外の「内分点」の求め方は疑問だよね

うん、あと「外分点」はあまりイメージできない、、
そこで今回、「文系数学における内分・外分の求め方」をご紹介します!
それではどうぞ!
内分点・外分点の意味
図を使って説明します!
内分の定義
線分\(\displaystyle AB\)を\(\displaystyle {\color{red}{m:n}}\)に内分する点\(\displaystyle P\)を図示する。
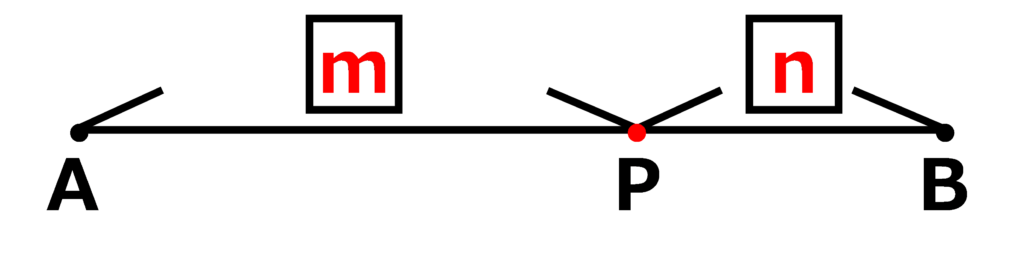

もし中点だったら、\(\displaystyle m:n={\color{red}{1:1}}\)にすれば良いね!
外分の定義
線分\(\displaystyle AB\)を\(\displaystyle {\color{red}{m:n}}\)に外分する点\(\displaystyle Q\)を図示する。



あれ?2種類ある?
これは例題で確かめてみましょう!
線分\(\displaystyle AB\)を\(\displaystyle {\color{red}{3:1}}\)に外分する点\(\displaystyle Q\)を図示する。

線分\(\displaystyle AB\)を\(\displaystyle {\color{red}{1:3}}\)に外分する点\(\displaystyle Q\)を図示する。

上の2つの例題から、次のことが分かりますね!
\(\displaystyle m{\color{red}{>}}n\)のとき、点\(\displaystyle Q\)は線分\(\displaystyle AB\)の右側 \(\displaystyle m{\color{blue}{<}}n\)のとき、点\(\displaystyle Q\)は線分\(\displaystyle AB\)の左側

迷ったら、\(\displaystyle AQ:QB=m:n\)にするために、点\(\displaystyle Q\)をどこに置くべきかを考えれば良い!
「パターン別」内分点・外分点の求め方
さて、いよいよ公式をご紹介したいと思います!
先程の線分\(\displaystyle AB\)を内分・外分する点\(\displaystyle P, Q\)の求め方は、
線分と点が「座標」「ベクトル」にあるときで異なるので、それぞれご紹介します!
線分が「座標」にあるとき
点\(\displaystyle A(x_{A}, y_{A})\)、点\(\displaystyle B(x_{B}, y_{B})\)のとき、
線分\(\displaystyle AB\)を\(\displaystyle m:n\)に内分する点\(\displaystyle P\)の座標は、\(\displaystyle \left(\frac{nx_{A}+mx_{B}}{m+n}, \frac{ny_{A}+my_{B}}{m+n}\right)\)
線分\(\displaystyle AB\)を\(\displaystyle m:n\)に外分する点\(\displaystyle Q\)の座標は、\(\displaystyle \left(\frac{-nx_{A}+mx_{B}}{m-n}, \frac{-ny_{A}+my_{B}}{m-n}\right)\)

ちなみに、空間座標でもできます!\(\displaystyle (x, y, {\color{red}{z}})\)のような形にすれば良いだけです!
線分が「ベクトル」であるとき
点\(\displaystyle A\)の位置ベクトルを\(\displaystyle \overrightarrow{a}\)、点\(\displaystyle B\)の位置ベクトルを\(\displaystyle \overrightarrow{b}\)とする。
線分\(\displaystyle AB\)を\(\displaystyle m:n\)に内分する点\(\displaystyle P\)の位置ベクトルは、\(\displaystyle \overrightarrow{p}=\frac{n\overrightarrow{a}+m\overrightarrow{b}}{m+n}\)
線分\(\displaystyle AB\)を\(\displaystyle m:n\)に外分する点\(\displaystyle Q\)の座標は、\(\displaystyle \overrightarrow{q}=\frac{-n\overrightarrow{a}+m\overrightarrow{b}}{m-n}\)

「パターン別」で異なるといっても、形はほぼ同じですね
「ベクトル」を使った、公式の導出

公式は分かったけど、なんでこうなるの?
最後に、公式の仕組みをお伝えします!
「内分」の導出
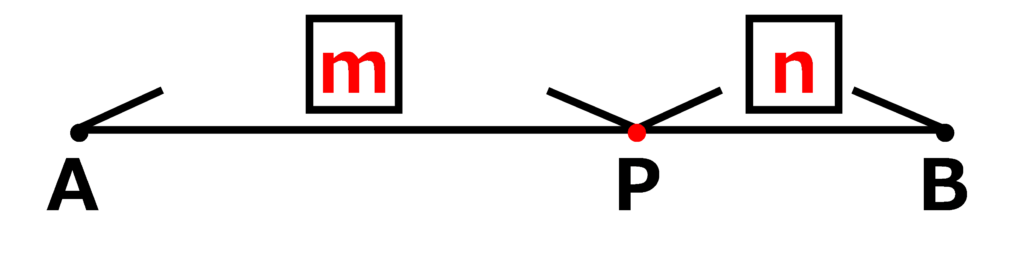
上図を「ベクトル」上にあると仮定する。
\(\displaystyle \overrightarrow{AP}=\frac{m}{m+n}\overrightarrow{AB}\)なので、
\(\displaystyle \overrightarrow{p}-\overrightarrow{a}=\frac{m}{m+n}\overrightarrow{b}-\overrightarrow{a}\)
\(\displaystyle \overrightarrow{p}={\color{red}{\frac{n\overrightarrow{a}+m\overrightarrow{b}}{m+n}}}\)
「外分」の導出

上図を「ベクトル」上にあり、\(\displaystyle {\color{red}{m>n}}\)とする。
\(\displaystyle \overrightarrow{AQ}=\frac{m}{m-n}\overrightarrow{AB}\)なので、
\(\displaystyle \overrightarrow{q}-\overrightarrow{a}=\frac{m}{m-n}\overrightarrow{b}-\overrightarrow{a}\)
\(\displaystyle \overrightarrow{q}={\color{red}{\frac{-n\overrightarrow{a}+m\overrightarrow{b}}{m-n}}}\)

公式なので丸暗記でもかまいませんが、忘れたとき用に式を覚えておきましょう!
まとめ
- 内分と外分は、「座標」「ベクトル」上で使われる
- 「座標」
線分\(\displaystyle AB\)を\(\displaystyle m:n\)に内分する点\(\displaystyle P\)の座標は、\(\displaystyle \left(\frac{nx_{A}+mx_{B}}{m+n}, \frac{ny_{A}+my_{B}}{m+n}\right)\)
線分\(\displaystyle AB\)を\(\displaystyle m:n\)に外分する点\(\displaystyle Q\)の座標は、\(\displaystyle \left(\frac{-nx_{A}+mx_{B}}{m-n}, \frac{-ny_{A}+my_{B}}{m-n}\right)\) - 「ベクトル」
線分\(\displaystyle AB\)を\(\displaystyle m:n\)に内分する点\(\displaystyle P\)の位置ベクトルは、\(\displaystyle \overrightarrow{p}=\frac{n\overrightarrow{a}+m\overrightarrow{b}}{m+n}\left({\color{red}{\overrightarrow{AP}=\frac{m}{m+n}\overrightarrow{AB}より}}\right)\)
線分\(\displaystyle AB\)を\(\displaystyle m:n\)に外分する点\(\displaystyle Q\)の座標は、\(\displaystyle \overrightarrow{q}=\frac{-n\overrightarrow{a}+m\overrightarrow{b}}{m-n}\left({\color{red}{\overrightarrow{AQ}=\frac{m}{m-n}\overrightarrow{AB}より}}\right)\) - 外分の際は、外分点の左右の位置に注意


