1⃣ □にあてはまる数を求めなさい。
(1) \(\displaystyle\frac{5}{7}\times0.84+0.32\div\frac{4}{5}=□\)
\(\displaystyle\frac{5}{7}\times\frac{84}{100}+\frac{32}{100}\times\frac{5}{4}=□\)
\(\displaystyle\frac{12}{20}+\frac{8}{20}=□\)
\(\displaystyle□=\color{red}{1}\)
(2) \(\displaystyle88\times\frac{7}{2}-(□-3)\div6\frac{2}{3}=5\)
\(\displaystyle44\times7-(□-3)\div\frac{20}{3}=5\)
\(\displaystyle-(□-3)\div\frac{20}{3}=5-44\times7\)
\(\displaystyle-(□-3)\div\frac{20}{3}=-303\)
\(\displaystyle-(□-3)=-303\times\frac{20}{3}\)
\(\displaystyle□-3=101\times20\)
\(\displaystyle□=\color{red}{2023}\)
(3) \(\displaystyle1977+1982+1991+1996+2000+2004+2009+2018+2023=□\)
\(\displaystyle(1977+2023)+(1982+2018)+(1991+2009)+(1996+2004)+2000=□\)
\(\displaystyle4000+4000+4000+4000+2000=□\)
\(\displaystyle□=\color{red}{18000}\)
(4) 底面が1辺150cmの正方形で、高さが70cmの四角柱の体積は□Lです。
\(\displaystyle150\times150\times70=1575000cm^{3}\)
1000cm^{3}=1Lなので、
\(\displaystyle□=1575000\div1000=\color{red}{1575}\)
(5) 原価□円の商品に15%の利益を見込んで定価をつけましたが、売れなかったため300円引きで売ったところ、5%の損失になりました。
\(\displaystyle□\times(1+0.15)-300=□\times(1-0.05)\)
\(\displaystyle□\times1.15-300=□\times0.95\)
\(\displaystyle□\times1.15-□\times0.95=300\)
\(\displaystyle□\times0.2=300\)
\(\displaystyle□=300\div0.2=\color{red}{1500}\)
(6) 下の筆算の㋐~㋕には、3から8までの6個の数字がそれぞれ1つずつ入ります。㋐~㋒、㋓~㋕はそれぞれ位が下がる(右に行く)につれて数字が大きくなり、㋐と㋓のように同じ位の(上下に並んだ)数字はいずれも上の数字の方が大きくなります。このとき、㋐に入る数字は□です。
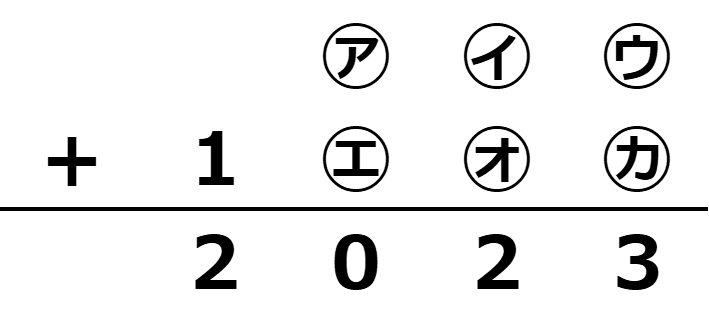
まず、最も数の大きい8は、㋒と㋕のいずれかに入る。
さらに、上の数の方が大きいため、㋒=8となる。
また、㋒の8と㋕を足したら、13となる。
このことから、㋕=5となる。
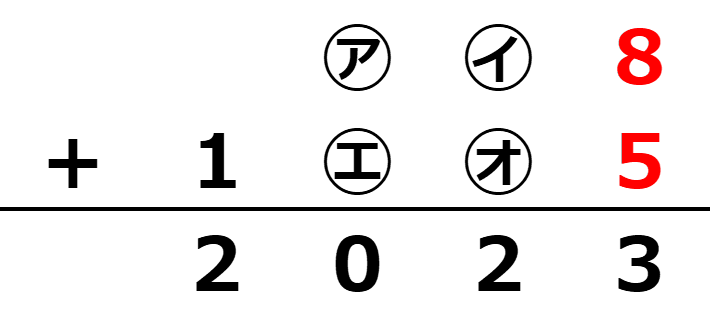
次に、㋑と㋔を考える。
㋑と㋔と一の位で繰り上がった1を足すと、12になる。
つまり、㋑+㋔=11となる㋑と㋔の組み合わせを考える。
組み合わせは、3と8、4と7、5と6の場合があるが、8と5は既に使用。
そのため、㋑=7、㋔=4(㋑の方が大きい)となる。
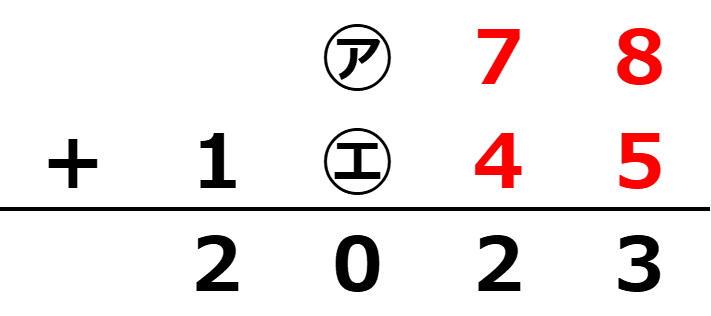
最後に、残りの6と3を、㋐と㋓のいずれかに入れる。
㋐の方が数は大きいため、㋐=6、㋓=3
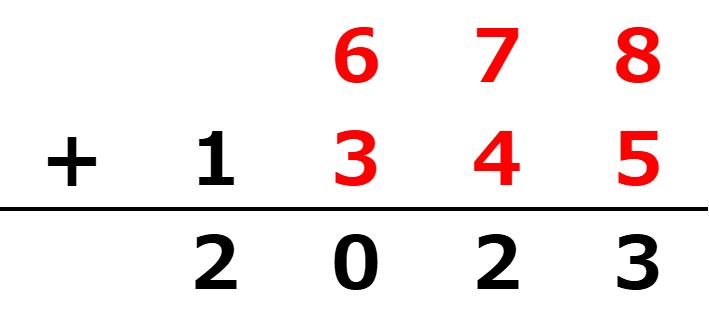
よって、□=6
(7) 1周1500mの池の周りを、Aさんは一定の速さで走って、Bさんは分速□mで歩いて進みます。2人が同じ場所から同時に出発し、同じ方向に進むと10分後にAさんはBさんにはじめて追いつき、反対方向に進むと6分後に出会います。
Aさんの速さを分速△m、Bさんの速さを分速□mとする。
2人とも同じ方向に進む場合、10分後にAさんはBさんと1周分(1500m)の差をつけているため、
\(\displaystyle△\times10-□\times10=1500\)
\(\displaystyle△\times10=□\times10+1500\)
\(\displaystyle△=□+150\)・・・①
また、1500mを互いに反対方向に進むと、2人は6分後に出会うため、
\(\displaystyle△\times6+□\times6=1500\)
この式の△に、①の式を入れる
\(\displaystyle(\color{red}{□+150})\times6+□\times6=1500\)
\(\displaystyle□\times6+900+□\times6=1500\)
\(\displaystyle□\times12=600\)
\(\displaystyle□=\color{red}{50}\)


