(1) 6%の食塩水200gに20%の食塩水を何gか混ぜると、濃度が15%になりました。この15%の食塩水に、2.5%の食塩水240gを混ぜると何%の食塩水になりますか?
20%の食塩水を□gとすると、
\(\displaystyle\frac{6}{100}\times200+\frac{20}{100}\times□=\frac{15}{100}\times(200+□)\)
\(\displaystyle12+\frac{20}{100}\times□=30+\frac{15}{100}\times□\)
\(\displaystyle\frac{20}{100}\times□-\frac{15}{100}\times□=30-12\)
\(\displaystyle\frac{5}{100}\times□=18\)
\(\displaystyle□=18\times\frac{100}{5}=360\)
この15%の食塩水560g(200g+360g)と2.5%の食塩水240gを混ぜると、
\(\displaystyle\frac{15}{100}\times560+\frac{2.5}{100}\times240\)
\(=84+6=90\)
食塩水800g(560g+240g)の中に、90g の食塩が含まれるので、
\(90\div800\times100=11.25\) 11.25%
(2) ある商店では、3種類の商品A,B,Cを売っています。AとBの商品の値段の和はCの3個分の値段より500円高いです。来月から商品の値段がすべて100円ずつ上がり、AとBとCの値段の比は4:3:2となります。現在のAの値段はいくらですか。ただし、消費税は考えないものとします。
商品A,B,Cの値段をそれぞれA,B,Cとする。
\(A+B=C\times3+500\)・・・①
上記の式のBとCをAと置き換える。
100円値上がりしたAとBとCの値段の比は4:3:2なので、
\(\displaystyle A+100:B+100=4:3\)
\(\displaystyle3\times(A+100)=4\times(B+100)\)
\(\displaystyle B\times4=A\times3-100\)
\(\displaystyle\color{red}{B}=A\times\frac{3}{4}-25\)・・・②
\(\displaystyle A+100:C+100=4:2\)
\(\displaystyle2\times(A+100)=4\times(C+100)\)
\(\displaystyle A\times2+200=C\times4+400\)
\(\displaystyle C\times4=A\times2-200\)
\(\displaystyle\color{red}{C}=A\times\frac{1}{2}-50\)・・・③
①の式に、②と③を代入する。
\(\displaystyle A+(A\times\frac{3}{4}-25)=(A\times\frac{1}{2}-50)\times3+500\)
\(\displaystyle A+A\times\frac{3}{4}-25=A\times\frac{3}{2}-150+500\)
\(\displaystyle A+A\times\frac{3}{4}-A\times\frac{3}{2}=-150+500+25\)
\(\displaystyle A\times\frac{1}{4}=375\)
\(\displaystyle A=\color{red}{1500円}\)
(3) ある公園の周りを1周する道路に等間かくに旗を立てます。120本立てた場合と180本立てた場合では、旗と旗の間かくは6mの差があります。144本立てたとき、旗と旗の間かくは何mになるか答えなさい。
180本の時の間かくを□mとする。
120本の時の間かくは(□+6)mとなる。
これを式にすると、以下のようになる。
\((□+6)\times120=□\times180\)
\(□\times120+720=□\times180\)
\(□\times60=720\)
\(□=12\)
144本立てたときの旗と旗の間かくを、再び□mとする。
\(□\times144=12\times180\)
\(□=\color{red}{15m}\)
(4) 今、袋の中に赤いボールがたくさん入っています。この袋の中に白いボールを27個入れてよく混ぜて無造作に70個のボールを取り出すと、その中に白いボールが14個含まれていました。このことから、初めに赤いボールは袋の中に何個入っていたと考えられますか。
無造作に取り出されたボールから、赤いボールと白いボールの比率が分かる。
\(赤:白=70-14:14=56:14=4:1\)
そのため、白いボールが27個のときの赤いボールを□個とする。
\(4:1=□:27\)
\(□=4\times27=\color{red}{108個}\)
(5) A,B,C,D,E,Fの6人は、文化祭のポスターを3人、2人、1人の3つの班に分かれてはります。そのとき、AとBは同じ班で、CとDは別々の班に分かれました。このとき、3人、2人、1人の分け方は何通りあるか答えなさい。
(i)AとBが3人班にいるとき
ABCが同じ→(ABC)(DE)(F)、(ABC)(DF)(E)、(ABC)(EF)(D) 3通り
ABDが同じ→(ABD)(CE)(F)、(ABD)(CF)(E)、(ABD)(EF)(C) 3通り
AB,C,Dが別々→(ABE)(CF)(D)、(ABF)(CE)(D)、(ABE)(DF)(C)、(ABF)(DE)(C) 4通り
(ii)AとBが2人班にいるとき
(DEF)(AB)(C)、(CEF)(AB)(D) 2通り
(i)(ii)より、\(3+3+4+2=\color{red}{12通り}\)
(6) 図のように、円Oは正方形ABCDの4つの辺と直角二等辺三角形EFCの3つの辺のすべてに接しています。このとき、角xの大きさを求めなさい。
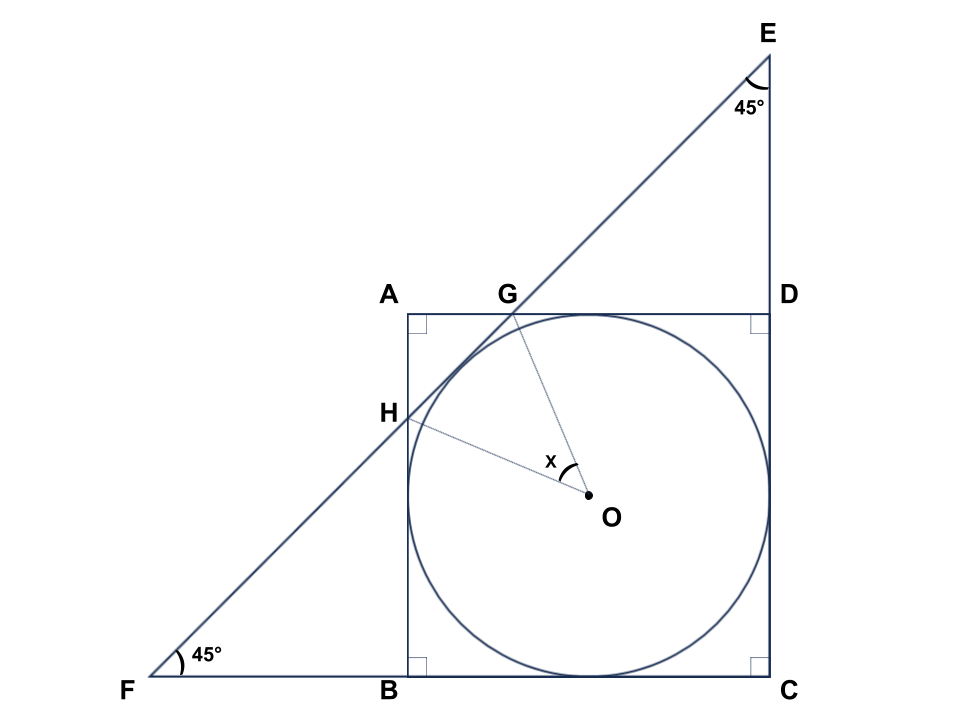
まず、上図のような90°や45°を使って、他の角度を埋めてみます。
そうすると、下図のようになります。
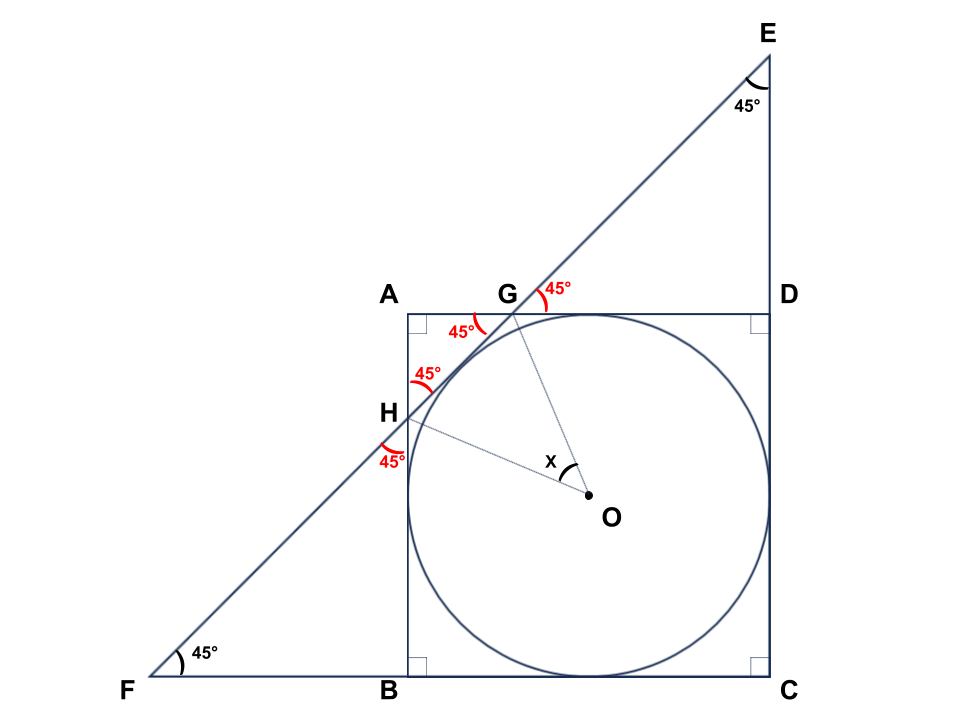
三角形AGHが直角二等辺三角形であることが分かりました。
さらに、下図のように、点Oから3つの接点に対して垂線(垂直な線)を引きます。
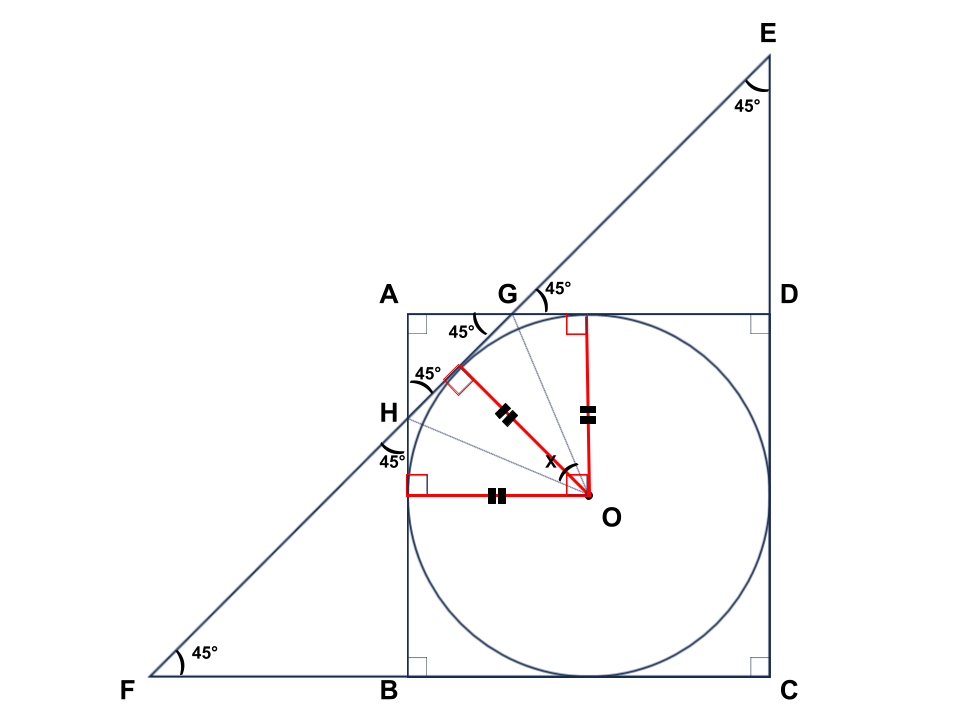
垂線は3つとも等しく、真ん中の垂線は直角二等辺三角形AHGの辺HGの真ん中を通るため、
3つの垂線に囲まれた2つの四角形は同じ形・大きさである。
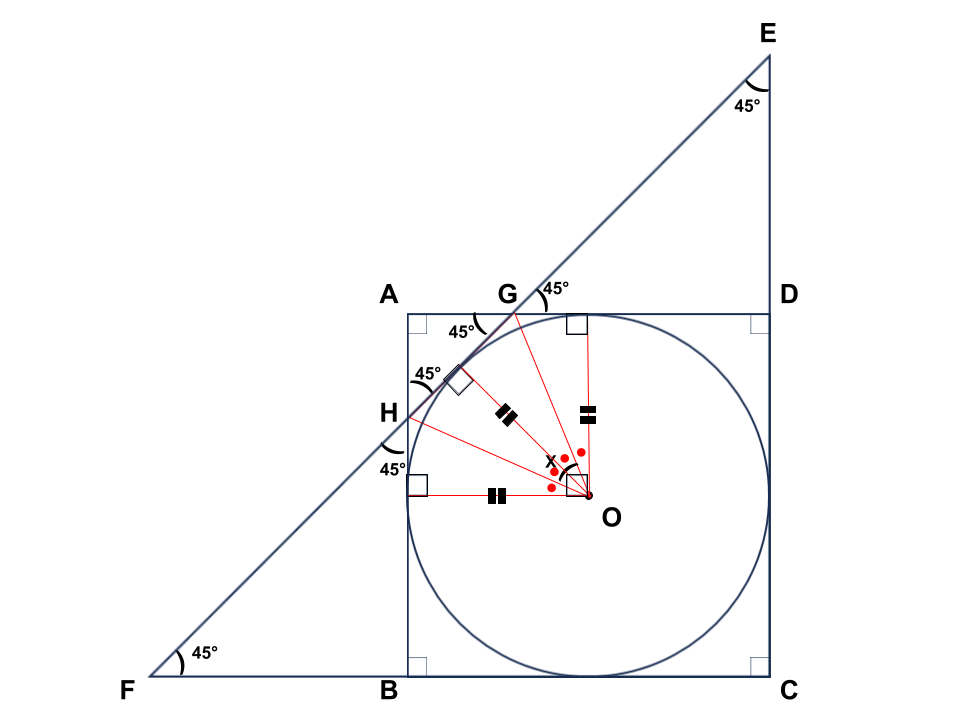
その2つの四角形を、OGとOHによってさらに2等分し、合計4つの三角形を作る。
この三角形同士も形・大きさが等しいので、点Oの90°を4等分(赤丸4つ)することができる。
角xはそのうちの赤丸2つ分に相当するので、
\(\displaystyle90°\times\frac{2}{4}=\color{red}{45°}\)


