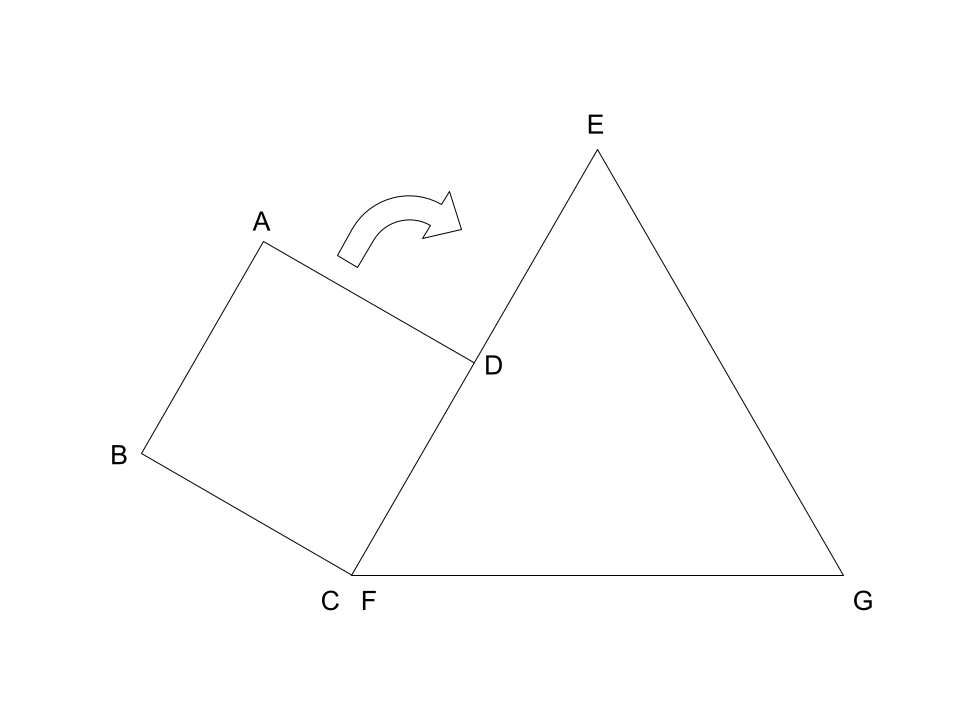
(1) 1辺の長さが2cmの正方形ABCDと1辺の長さが4cmの正三角形EFGがあります。
最初は図のように点Cと点Fの位置が一致し、点Dは辺EF上にあります。
ここから正方形ABCDが正三角形EFGの周りを辺FE, EG, GFに沿って矢印の向きにすべることなく
回転しながら正方形のそれぞれの頂点が元の位置になるまで移動を続けます。
このとき、点A, B, C, Dのうち、点Gを通る点をすべて記号で答えなさい。
【解説】
正方形ABCDが矢印の方向に90℃ずつ回転していくと、初めの1回転は以下のようになる。
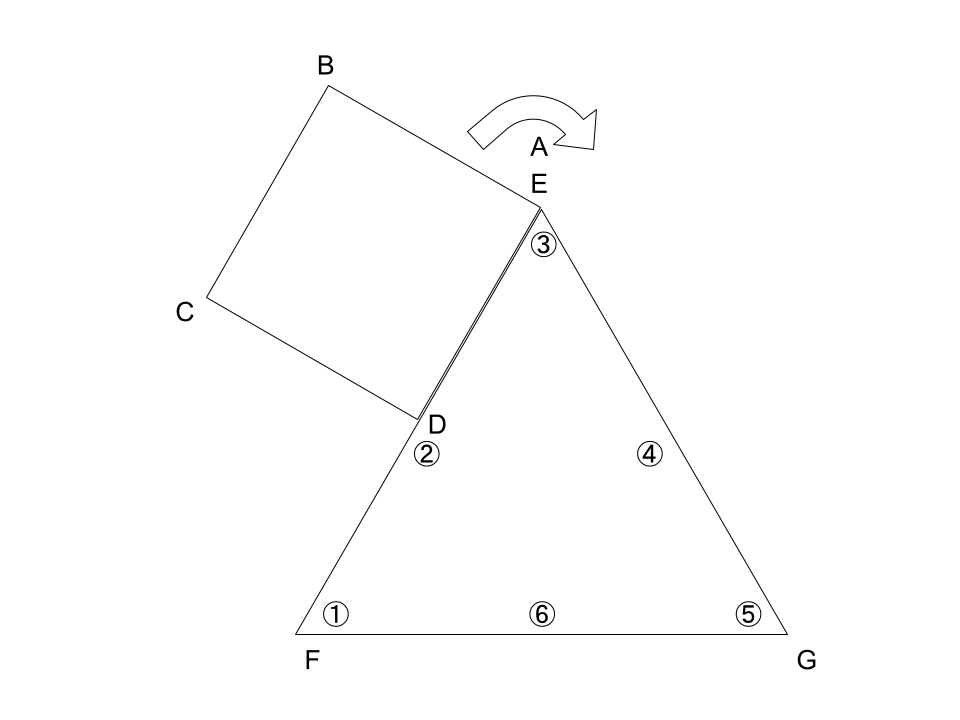
点Aが点Eに重なるようになる。
上図の、①と②にそれぞれCとDが戻ってくるまで回転させる。
それまで、①~⑥を通過する点の軌跡を、これから1周ごとに紹介していく!
『1周目』
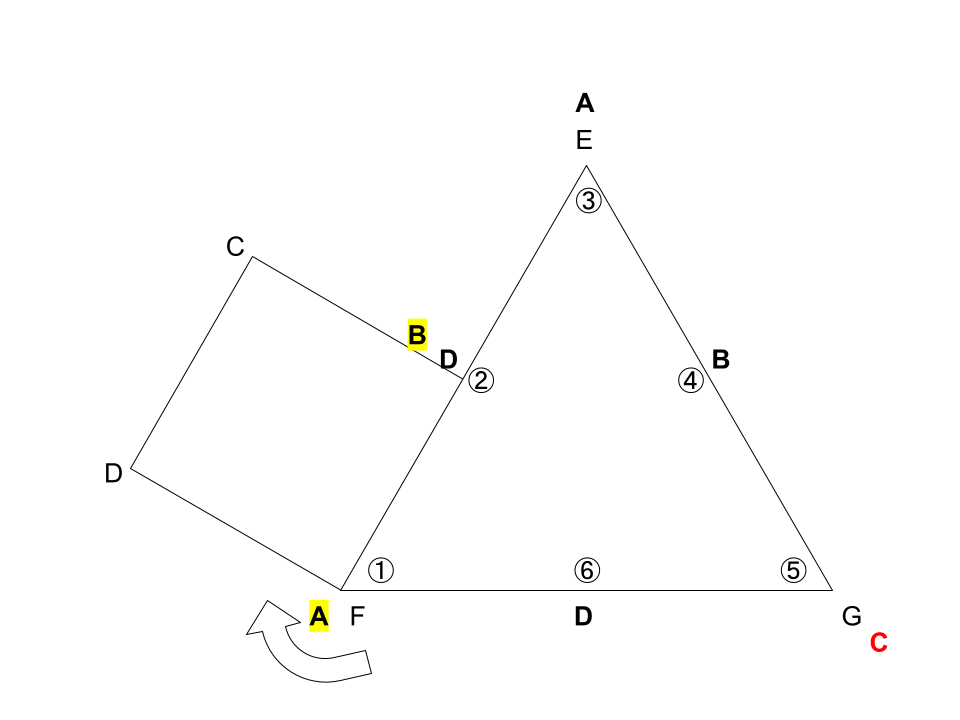
黒い太字→①~⑥の位置に来た点
黄色マーカーの太字→正方形ABCDが元の位置に戻ってきた時の、①と②の位置にある点
赤い太字→点Gに来た点(この問題の答え!)
『2周目』
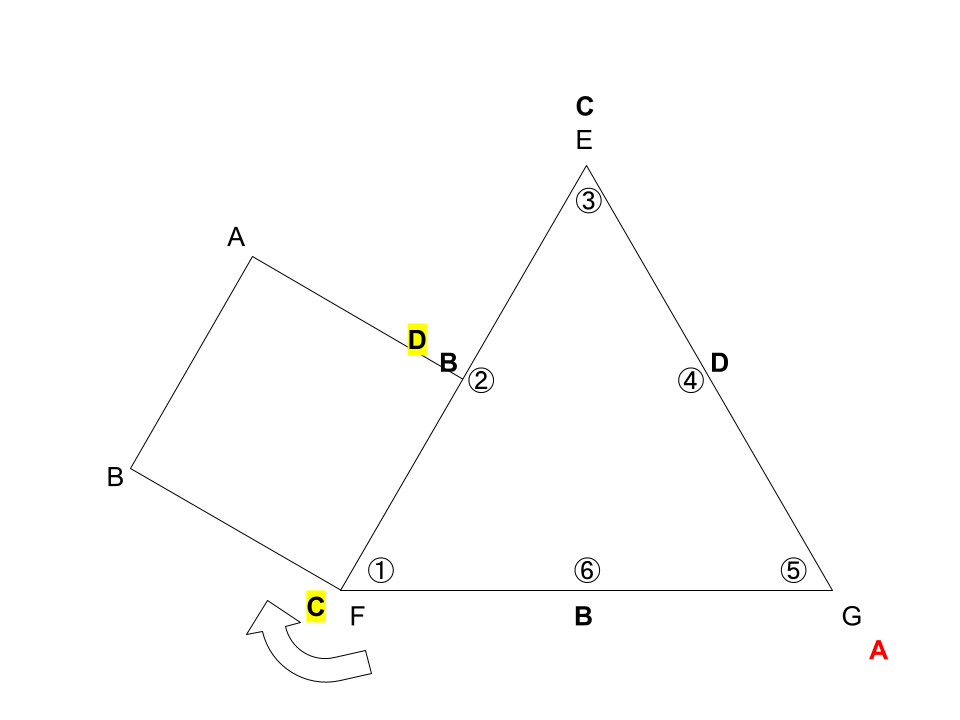
①と②にそれぞれCとD(黄色マーカー)が戻ってきたため、1周目と2周目で点Gに来た点を答える!
答えは、点AとC


