次の図形の周の長さを求めなさい。
(1)
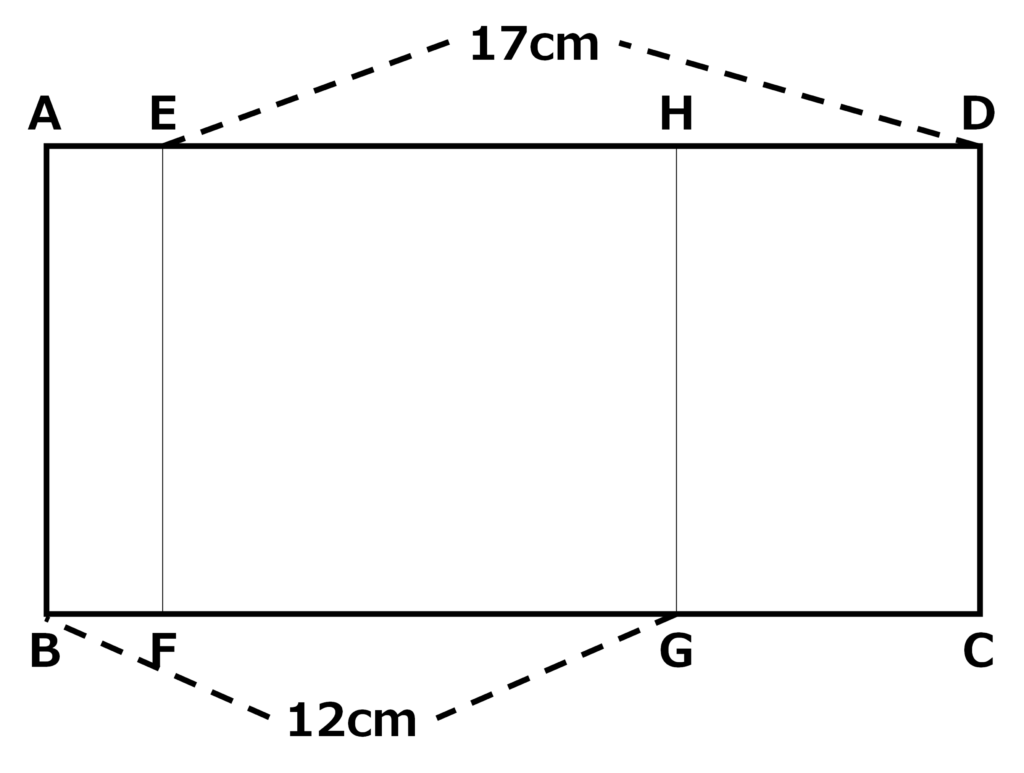
(ただし四角形ABCDは長方形、四角形EFGHは正方形)
AB=□cmとする。
四角形ABCDの周の長さは、
\(\displaystyle□(\color{red}{AB})+\{12+(17-□)\}(\color{red}{BC})+□(\color{red}{CD})+\{17+(12-□)\}(\color{red}{DA})\)
\(\displaystyle=□+12+17-□+□+17+12-□\)
\(\displaystyle=12+17+17+12=\color{red}{58cm}\)
(2)

(ただし四角形ABCD、ECFGはともに正方形)
正方形のECFGの1辺を□cmとする。
上の図形の周の長さは、
\(\displaystyle(□+4)(\color{red}{AB})+14(\color{red}{BF})+□(\color{red}{FG})+□(\color{red}{GE})+4(\color{red}{ED})+(□+4)(\color{red}{DA})\)
\(\displaystyle=□+4+14+□+□+4+□+4\)
\(\displaystyle=□\times4+26\)・・・①
\(BC=CD\)より、
\(\displaystyle14-□(BC=\color{red}{BF-CF})=□+4(CD=\color{red}{CE+DE})\)
\(\displaystyle□\times2=14-4\)
\(\displaystyle□=10\div2=5\)・・・②
②を①に入れる。
\(\displaystyle=5\times4+26=20+26=\color{red}{46cm}\)


