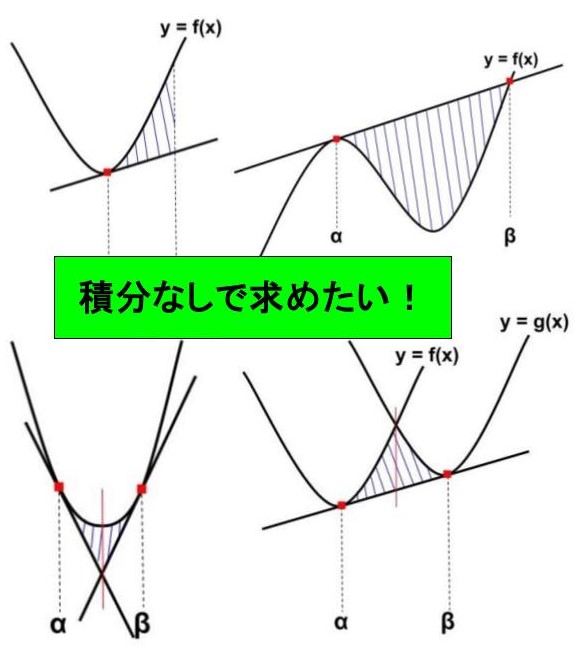
皆さんは、積分の面積を求める際に便利な「1/6・1/3・1/12公式」をご存じですか?
例えば、「放物線と直線で囲まれた面積を求めよ」と言われたら、どう解きますか?
「2線の共有点を求める」
「共有点を使って、\(\displaystyle \int_α^β f(x)dx\)の式を作る」
「\(\displaystyle f(x)\)を積分させる」
「積分後の\(\displaystyle f(x)\)に、\(\displaystyle α\)と\(\displaystyle β\)を代入する」
「両者の差を求める」
かなりめんどくさいですよね?
特に、積分後の式は次数が大きいため、\(\displaystyle α\)や\(\displaystyle β\)を代入しようと思ったら、心が折れます(´;ω;`)
しかし、今回の公式を使えば、万事解決です!
そこで今回は、
「積分の面積を求める上での裏技:1/6・1/3・1/12公式とは何か?」についてご紹介します!
この記事は、以下の方々向けです!
- 積分の問題を短縮させたい人
- 共通テスト数学で時間がなくて困っている人
公式暗記のために知っておきたいこと
交点の数に注目!積分前の次数を求める!
早速、以下の図を見てみましょう!
\(\displaystyle f(x)=x^{2}-2x+1\)
\(\displaystyle g(x)=2x-2\)
\begin{eqnarray} {\color{red}{g(x)-f(x)}} &=& 2x-2-(x^{2}-2x+1) \\ &=& -x^{{\color{red}{2}}}+4x-3 \end{eqnarray}
このように、交点が2つのとき、
面積を求めるための\(\displaystyle \int_α^β \{g(x)-f(x)\}dx\)の\(\displaystyle {\color{red}{g(x)-f(x)}}\)は2次式であることが分かります!
積分後の次数は増える!
以下の計算式を見てみましょう!
\begin{eqnarray} \int x^{2}dx=\frac{1}{3}x^{3}+C\end{eqnarray}
\begin{eqnarray} \int (x-a)^{2}dx=\frac{1}{3}(x-a)^{3}+C\end{eqnarray}
このように、\(\displaystyle \int\)の中の\(\displaystyle {\color{red}{g(x)-f(x)}}\)が2次式であれば、計算結果は3次式になります!
まとめると、今回の1/6・1/12・1/3公式を覚えるにあたって、以下がポイントです!
2つの線同士の交点がn個 ⇒ 計算結果は(n+1)乗
公式一覧
1/6公式
放物線(二次関数)・直線(一次関数)|2次ー1次型
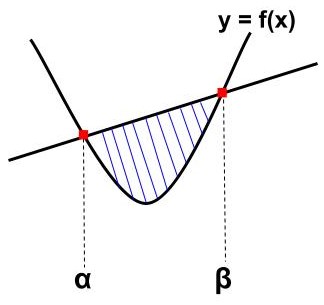
交点:2つ
放物線:\(\displaystyle\LARGE f(x)={\color{red}{a}}x^{2}+bx+c\)
\begin{eqnarray}\LARGE S=\frac{|{\color{red}{a}}|}{6}(β-α)^{{\color{red}{3}}} \end{eqnarray}
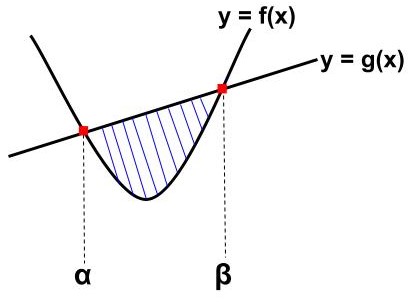
放物線・放物線|2次ー2次型
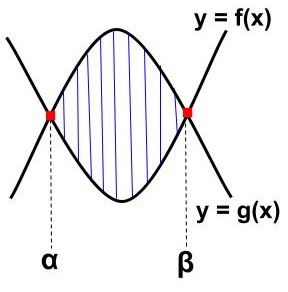
交点:2つ
放物線①:\(\displaystyle\LARGE f(x)={\color{red}{a}}x^{2}+bx+c\)
放物線②:\(\displaystyle\LARGE g(x)={\color{red}{d}}x^{2}+ex+f\)
\begin{eqnarray}\LARGE S=\frac{|{\color{red}{d-a}}|}{6}(β-α)^{{\color{red}{3}}} \end{eqnarray}
1/3公式
放物線・直線|2次ー1次(接線)型
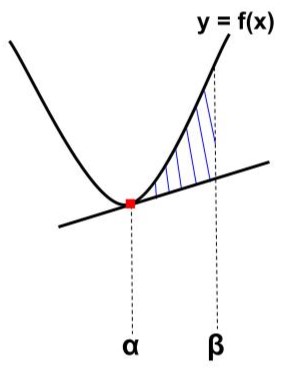
交点:2つ(重解)
放物線:\(\displaystyle\LARGE f(x)={\color{red}{a}}x^{2}+bx+c\)
\begin{eqnarray}\LARGE S=\frac{|{\color{red}{a}}|}{3}(β-α)^{{\color{red}{3}}} \end{eqnarray}
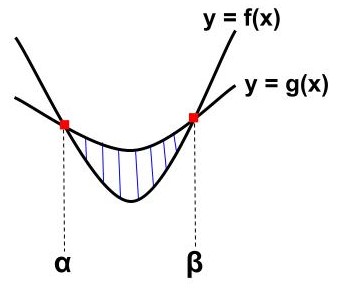
放物線・放物線|2次ー2次(接線)型
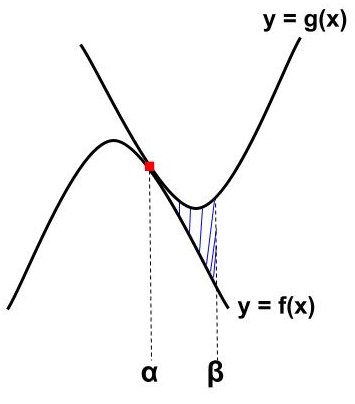
交点:2つ(重解)
放物線①:\(\displaystyle\LARGE f(x)={\color{red}{a}}x^{2}+bx+c\)
放物線②:\(\displaystyle\LARGE g(x)={\color{red}{d}}x^{2}+ex+f\)
\begin{eqnarray}\LARGE S=\frac{|{\color{red}{d-a}}|}{3}(β-α)^{{\color{red}{3}}} \end{eqnarray}
1/12公式
三次関数・直線|3次ー1次(接線)型
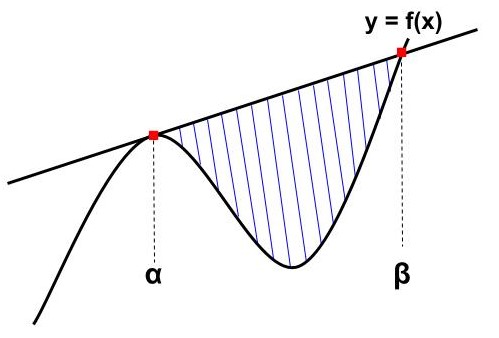
交点:3つ(重解2つ+1つ)
三次関数:\(\displaystyle\LARGE f(x)={\color{red}{a}}x^{3}+bx^{2}+cx+d\)
\begin{eqnarray}\LARGE S=\frac{|{\color{red}{a}}|}{12}(β-α)^{{\color{red}{4}}} \end{eqnarray}
放物線・直線・直線|2次ー1次(接線)ー1次(接線)型
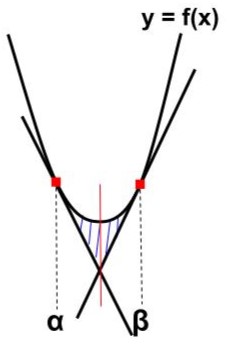
交点:2つ(重解)→上図の赤い線で分けると、2次ー2次(接線)型になる!
放物線:\(\displaystyle\LARGE f(x)={\color{red}{a}}x^{2}+bx+c\)
\begin{eqnarray}\LARGE S=\frac{|{\color{red}{a}}|}{12}(β-α)^{{\color{red}{3}}} \end{eqnarray}
放物線・放物線・直線|2次ー2次ー1次(接線)型
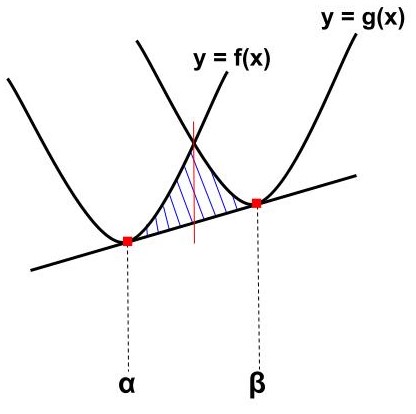
交点:2つ(重解)→上図の赤い線で分けると、2次ー2次(接線)型になる!
放物線①:\(\displaystyle\LARGE f(x)={\color{red}{a}}x^{2}+bx+c\)
放物線②:\(\displaystyle\LARGE f(x)={\color{red}{a}}x^{2}+ex+f\)
※\(\displaystyle f(x)\)と\(\displaystyle g(x)\)は傾きが同じ
\begin{eqnarray}\LARGE S=\frac{|{\color{red}{a}}|}{12}(β-α)^{{\color{red}{3}}} \end{eqnarray}
例題とポイント
\(\displaystyle y=-\frac{1}{2}x^{2}+2x+5\)のグラフと\(\displaystyle y=x+1\)のグラフに囲まれた部分の面積を求めなさい。
二次関数と一次関数なので、以下のような1/6公式が使えます!
\begin{eqnarray}\LARGE S=\frac{|a|}{6}(β-α)^3 \end{eqnarray}
この\(\displaystyle S\)を求めるには、
\(\displaystyle a\):二次関数の係数、\(\displaystyle β\):大きい方の解、\(\displaystyle α\):小さい方の解
を代入する必要があります!
\begin{eqnarray} -\frac{1}{2}x^{2}+2x+5=x+1・・・{\color{red}{式①}} \end{eqnarray}
\begin{eqnarray} (-\frac{1}{2}x^{2}+2x+5)-(x+1)=0 \end{eqnarray}
\begin{eqnarray} {\color{blue}{-\frac{1}{2}}}x^{2}+x+4=0・・・{\color{red}{式②}} \end{eqnarray}
\begin{eqnarray} x^{2}-2x-8=0 \end{eqnarray}
\begin{eqnarray} (x+2)(x-4)=0 \end{eqnarray}
\begin{eqnarray} x={\color{blue}{-2}},{\color{blue}{4}} \end{eqnarray}
青字の数字を1/6公式に代入します!
\begin{eqnarray} S = \frac{|a|}{6}(β-α)^3 \end{eqnarray}
\begin{eqnarray} =\frac{|{\color{blue}{-\frac{1}{2}}}|}{6}\{{\color{blue}{4}}-({\color{blue}{-2}})\}^3 \end{eqnarray}
\begin{eqnarray} ={\color{red}{\frac{1}{2}}}\div6\times6^{3}・・・{\color{red}{式③}} \end{eqnarray}
\begin{eqnarray} =\frac{6^{3}}{2・6} \end{eqnarray}
\begin{eqnarray} =18 \end{eqnarray}
\begin{eqnarray}\LARGE S={\color{red}{18}} \end{eqnarray}
この問題でのポイントは2つあります!
式①から式②において、両辺に2をかけて分母を払ったりしないこと!
式③において、\(\displaystyle x^{2}\)の係数が\(\displaystyle ±\)どちらであろうと、絶対値の記号により\(\displaystyle a\)を正として計算すること!
1つ目のポイントに関しては、両辺にかけたり割ったりして、\(\displaystyle x^{2}\)の係数を変えないように注意してください!
まとめ
いかがでしたか?
公式暗記のポイントと公式一覧は、以下に再度まとめさせていただきます!
- 2つの線同士の交点がn個 ⇒ 計算結果は(n+1)乗
- 二次関数や三次関数の係数は、絶対値
- 交点を求める際の方程式の両辺に、かけたり割ったりしない
- 1/6公式 「2次ー1次型」+「2次ー2次型」
\begin{eqnarray}\LARGE S=\frac{|{\color{red}{a}}|}{6}(β-α)^3 \end{eqnarray}
\begin{eqnarray}\LARGE OR \end{eqnarray}
\begin{eqnarray}\LARGE S=\frac{|{\color{red}{d-a}}|}{6}(β-α)^3 \end{eqnarray}
- 1/3公式 「2次ー1次(接線)型」+「2次ー2次(接線)型」
\begin{eqnarray}\LARGE S=\frac{|{\color{red}{a}}|}{3}(β-α)^3 \end{eqnarray}
\begin{eqnarray}\LARGE OR \end{eqnarray}
\begin{eqnarray}\LARGE S=\frac{|{\color{red}{d-a}}|}{3}(β-α)^3 \end{eqnarray}
- 1/12公式 「2次ー1次(接線)ー1次(接線)型」「2次ー2次ー1次(接線)型」
+「3次ー1次(接線)型」
\begin{eqnarray}\LARGE S=\frac{|a|}{12}(β-α)^{\color{red}{3}} \end{eqnarray}
\begin{eqnarray}\LARGE OR \end{eqnarray}
\begin{eqnarray}\LARGE S=\frac{|a|}{12}(β-α)^{\color{red}{4}} \end{eqnarray}
特段、必ずしもこれらの公式を覚えなくても積分で導くことはできます。
また、公式を覚えるにしても、
「累乗は覚えられるけど、この線同士のときはこの分数(1/6か1/3か1/12)というのは難しくて覚えられない!」というような困難があると思います。
しかし、難関大学の二次試験では、計算が複雑な問題が出題され、これらの公式で大幅な時間短縮が望めます!
共通テストでは、面積を求める問題において積分の途中式を問われることは少なく、答えだけ求めればよいため、これらの公式はとても効果的です!
まずは、1/6公式から確実に覚えていきましょう!