はじめに
新課程による選択科目の変化
皆さんは、2025年度入試から出題内容や大問数が変更になるのはご存じでしょうか?
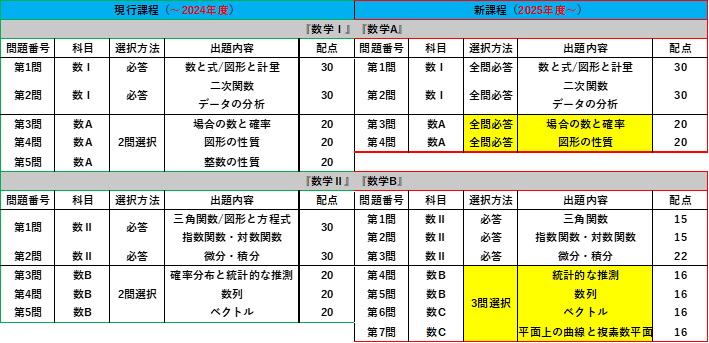
令和7年度大学入学者選抜に係る大学入学共通テスト 出題教科・科目の出題方法等
※以上の表は参考文献をもとに著者が作成
変更点は、主に以下のようです。
- 数学ⅠAにおける選択科目の消滅
- 数学C追加→数学ⅡBにおける選択科目の増加
- 試験時間が60分から70分へ
旧課程と比較して難易度は?
はっきり言って、難易度は上がるでしょう!
数学ⅠAと数学ⅡBで、それぞれ難易度が上がる根拠があります。
まず数学ⅠAに関して、「整数の性質」が消滅することです!
なぜなら、整数はパターンを把握すれば解ける問題だったからです。
パターンとして多いのが、「不定方程式の解をユークリッドの互除法で求める」というものです。
このパターンの解法を暗記していれば、安定して点を取ることができる分野でした。
反対に、生き残った「場合の数と確率」「図形の性質」は、その場のひらめきや調子が影響するため、
点数にむらが出やすいです。
最後に数学ⅡBに関して、「平面上の曲線と複素数平面」が追加されることです!
なぜなら、この単元はもともと数学Ⅲに属していたからです。
それが新課程では数学Cの1単元となり、文系受験生も勉強しなければならない分野となりました。
それでは、難化することが予想される「新課程の共通テストで対策すべき分野とは何か?」
ランキング形式でご紹介します!
第4位 数列
受験生の多くが苦手だと捉えがちな「数列」。
しかし、共通テストの場合、難易度はそれほどでもないんです!
少し問題を見てみましょう!
数列\(\displaystyle \{a_{n}\}\)が、
\[\displaystyle a_{n+1}-a_{n}=14(n=1,2,3,・・・)\]
を満たすとする。
\(\displaystyle a_{1}=10\)のとき、\(\displaystyle a_{2}={\color{red}{アイ}},\) \(a_{3}={\color{red}{ウエ}}\)である。
数列\(\displaystyle \{a_{n}\}\)の一般項は、初項\(\displaystyle a_{1}\)を用いて
\[\displaystyle a_{n}=a_{1}+{\color{red}{オカ}}(n-1)\]
と表すことができる。
2024年度大学入学共通テスト『数学Ⅱ・B』第4問(1)
上のように、「数列\(\displaystyle \{a_{n}\}\)の一般項」という最終的な答えにたどり着くために、
\(\displaystyle a_{1}=10\)と解く過程を教えてくれています!
再び問題を見てみましょう!
太郎さんは
\[\displaystyle (c_{n}+3)(2c_{n+1}-c_{n}+3)=0(n=1,2,3,・・・)・・・①\]
を満たす数列\(\displaystyle \{c_{n}\}\)について調べることにした。
\(\displaystyle (i)\)
・数列\(\displaystyle \{c_{n}\}\)が①を満たし、\(\displaystyle c_{1}=5\)のとき、\(\displaystyle c_{2}={\color{red}{サ}}\)である。
・数列\(\displaystyle \{c_{n}\}\)が①を満たし、\(\displaystyle c_{3}=-3\)のとき、\(\displaystyle c_{2}={\color{red}{シス}}\), \(\displaystyle c_{1}={\color{red}{セソ}}\)である。
・
・
・
(中略)
・
・
・
\(\displaystyle (iv)\) 次の\(\displaystyle (Ⅰ), (Ⅱ), (Ⅲ)\)は、数列\(\displaystyle \{c_{n}\}\)に関する命題である。
\(\displaystyle (Ⅰ)\) \(\displaystyle c_{1}=-3\)かつ\(\displaystyle c_{100}=-3\)であり、かつ①を満たす数列\(\displaystyle \{c_{n}\}\)がある。
\(\displaystyle (Ⅱ)\) \(\displaystyle c_{1}=-3\)かつ\(\displaystyle c_{100}=-3\)であり、かつ①を満たす数列\(\displaystyle \{c_{n}\}\)がある。
\(\displaystyle (Ⅲ)\) \(\displaystyle c_{1}=-3\)かつ\(\displaystyle c_{100}=3\)であり、かつ①を満たす数列\(\displaystyle \{c_{n}\}\)がある。
\(\displaystyle (Ⅰ), (Ⅱ), (Ⅲ)\)の真偽の組合せとして正しいものは\(\displaystyle {\color{red}{ト}}\)である。
2024年度大学入学共通テスト『数学Ⅱ・B』第4問(3)
数列の最後の問題(3)(iv)においても、前の問題(3)(i)にヒントが書かれているんです!
このように、1つ1つの問題の指示に従っていけば、全く難しいということはありません!
今まで苦手だと思っていた人も、怯まず対策していきましょう!
第3位 三角関数
三角関数における問題は、時間が足りないということです!
たとえ公式を覚えていても、
「計算が複雑!」「角度の範囲・πを使った分数が複雑!」
これらの理由から、想像より時間がかかってしまうのではないでしょうか?
そのため、自分の頭の中ですぐ知識を取り出せるように暗記の仕方を工夫したり、
問題の形式に慣れたりと、
時間短縮を狙うことで、点数アップにつなげやすい分野だと思います!
また、以下の2つの記事も参考にしてみてください!
1つ目は語呂合わせ、2つ目は図や式を使った暗記方法をご紹介しており、
共通テストにおけるスピードアップにおいても参考になると思います!
ぜひご参照ください!!
第2位 二次関数
以下の2つの理由があります!
- 頻出分野であり範囲が広い
- 最後に詰め込みやすい公式がある
まず1つ目の理由に関しては、数学ⅠAのみならずⅡBでも使われる分野であることです!
その例として、微分積分です!
2つ目の理由に関しては、覚えることで時短できる公式があることです!
問題を見てみましょう。
\(\displaystyle 0\text{≦}x\text{≦}1\)の範囲で、関数\(\displaystyle y=f(x)\)のグラフと\(\displaystyle x\)軸および\(\displaystyle y\)軸で囲まれた図形の面積を\(\displaystyle S_{1}\)、
\(\displaystyle 1\text{≦}x\text{≦}m\)の範囲で、関数\(\displaystyle y=f(x)\)のグラフと\(\displaystyle x\)軸で囲まれた図形の面積を\(\displaystyle S_{2}\)とする。
このとき、\(\displaystyle S_{1}={\color{red}{セ}}\)、\(\displaystyle S_{2}={\color{red}{ソ}}\)である。
ほぼ毎年、放物線(二次関数)と直線との間にできる図形の面積を求める問題が出題されます。
通常では時間がかかってしまうのですが、ある公式を使えば時短して求めることができます!
その例が、「1/3公式」「1/6公式」「1/12公式」です!

この公式を使えば、
・インテグラルなし!
・「1/3」「1/6」「1/12」といった分数を覚える!
これだけで面積を求められます!
後に記事として紹介させていただきます!
しかし、このような有難い公式を使いこなすには、1月に入ってからでは遅いです!
今のうちに練習しておくことをおすすめします!!
第1位 データの分析
以下の理由から、最優先で対策することがおすすめです!
- 周りの受験生はおろそかにしがち
- 対策範囲が狭い
まず、データの分析は2次試験ではほぼ使われないため、受験生は対策に時間をかけない傾向にあります。
そのため、ここで対策すれば周りと差をつけることができます!
また、範囲はそこまで広くないので、直前期だけでも対策することでだいぶ点数が上がります!

共通テストに「情報」科目が入ってきたのもあり、データ・情報系の知識がより重要視されているように感じます!
まとめ
4位 数列
3位 三角関数
2位 二次関数
1位 データの分析
いかがでしたか?
共通テストで大事なのは、「スピード」と「正確さ」です。
ただ、今回の4分野の勉強において、共通テストの形式慣れや公式の効果的な暗記をすれば、
どちらも制することができると思います!
共通テスト本番まで、残り1か月半ですが、気を抜かず走り切りましょう!!